Featured image of post 论文阅读 - ICML2025 高光论文选读
论文 计算机

论文阅读 - ICML2025 高光论文选读

什么人才能站着讲15分钟不冷场...(By Deepseek)

ICML

第 42 届 ICML 于 2025 年 7 月 13 日至 19 日在加拿大温哥华会议中心举行.

[Oral] 基于 SVD 学习伪造特征

AIGIs

AI 生成图像 (AI-Generated Images, AIGIs) 发展很快, 但也带来了潜在的巨大风险, 因此 AIGIs 的检测显得非常重要. 传统的方式是拿视觉基础模型 (Vision Foundation Model, VFM) 用二分类器, 预测图像被判定为虚假的可能性. 检测伪造的核心难点在于泛化. 现有的工作大概有两个方向:

  • 伪造模式 (fake pattern) 学习, 是最主流的一种, 通过某个变换函数把 $x$ 映射到 $x'$, 认为 $x'$ 的特征空间可以学到伪造模式. 然而, 鉴于现实世界中伪造方法的多样性不断增加, 试图详尽列举所有可能的伪造模式并 “期望” 在未见过的伪造方法上实现良好的泛化是不现实的. (原话)
  • 真实分布 (real distribution) 学习, 典型方法如单类异常检测, 提出一种误差作为得分, 来判断图像是否为伪造. 但这需要大量真实样本, 且通常属性分布不均衡的样本相当有限, 难以学习到真实图像的鲁棒表示.

Effort

论文 [] Unknown-material 认为, 发生过拟合现象的重要原因是简单训练的检测器尝试寻找到已见过的假图像模式的捷径, 导致特征空间实质降维为低秩结构, 限制了表达能力和泛化能力. 因此论文采用了 PCA 方法, 强制模型保留高秩结构.

基于此, 对于预训练权重矩阵 $W$ (一般的 VFM 权重矩阵都是方阵, 比如 ResNet), SVD 将其分解为 $W = U \Sigma V^\top$, 并采用秩-$r$ 近似 $W_r = U_r \Sigma_r V_r^\top $. 残差分量 $W - W_r = U_{n-r} \Sigma_{n-r} V_{n-r}^\top $ 是我们要学习的形式, 而 $U_r, \Sigma_r, V_r$ 则固定.

我们一方面希望 $\Delta W$ 捕捉真实与虚假之间有意义的差异, 一方面又希望优化 $\Delta W$ 是不改变 $W$ 整体的属性. 我们介绍 Effort 方法:

算法Effort

输入 > 预训练权重矩阵 $W \in \mathbb{R}^{n \times n}$, 秩 $r$, 训练集 $D = \{(x_i, y_i)\}_{i=1}^N$, 超参数 $\lambda_1, \lambda_2$.

输出 > 更新后的权重矩阵 $W$.

  1. 做 SVD 分解 $W = U \Sigma V^\top$.
  2. 取 $r$ 个主成分, 计算 $W_r = U_r \Sigma_r V_r^\top $, 保持不变.
  3. 对残差分量做 SVD: $\Delta W = W-W_r = U_{n-r} \Sigma_{n-r} V_{n-r}^\top $. 并记: $$ \hat{U} = \begin{bmatrix} U_r & U_{n-r} \end{bmatrix} \quad \hat{V} = \begin{bmatrix} V_r & V_{n-r} \end{bmatrix} $$
  4. 利用 $W=W_r+\Delta W$ 做前向传播, 计算损失 $\mathcal{L}_{\mathrm{cls}}$.
  5. 计算正交正则化损失 (用于保持奇异向量的正交性质): $$ \mathcal{L}_{\mathrm{ortho}} = \| \hat{U}^\top \hat{U} - I \|_F^2 + \| \hat{V}^\top \hat{V} - I \|_F^2 $$
  6. 计算奇异值约束损失 (用于控制奇异值的接近程度): $$ \mathcal{L}_{\mathrm{ksv}} = \left| \| \hat{W} \|_F^2 - \|W\|_F^2 \right| $$
  7. 计算总损失: $$ \mathcal{L} = \mathcal{L}_{\mathrm{cls}} + \lambda_1 \mathcal{L}_{\mathrm{ortho}} + \lambda_2 \mathcal{L}_{\mathrm{ksv}} $$
  8. 反向传播, 更新 $\Delta W$.
  9. 对每个 epoch 和 batch, 重复步骤 4-8.
  10. 返回更新后的权重矩阵 $W = W_r + \Delta W$.

Effort

论文推荐 $r=n-1$, 即只用一个特征向量来捕捉虚假图像的特征. 对其他的 $r$ 也有一定鲁棒性.

实验及可视化

Effort 展现了巨大的优势. 仅用了原本模型的约 0.1% ~ 1% 的训练参数量, 能带来高达 10 个点的提升.

论文还做了消融实验, 证明了正交正则化和奇异值约束对模型性能的作用. 架构默认采用 CLIP 作为 VFM, 但对其他 VFM 也有良好的适应性.

语义-真实性分解

值得一提的是论文给出的语义-虚假性分解可视化方案. 一般的网络只能给出虚假性分数, 但 Effort 可以实现对语义和虚假性的正交分解学习.

[Oral] 稀疏的 RL 网络可能更好

1000 * 10% > 100

一般深度学习中较大的模型通常能获得更好的结果, 但在深度强化学习 (Deep Reinforcement Learning, DRL) 中, 这种规模扩展模式会失效，增加模型大小往往会导致性能下降.

论文 [] Unknown-material 实际上是一篇实验报告稿, 它指出如果在扩大参数规模的同时, 保持网络的稀疏性, 可以有效避免性能崩溃和优化问题.

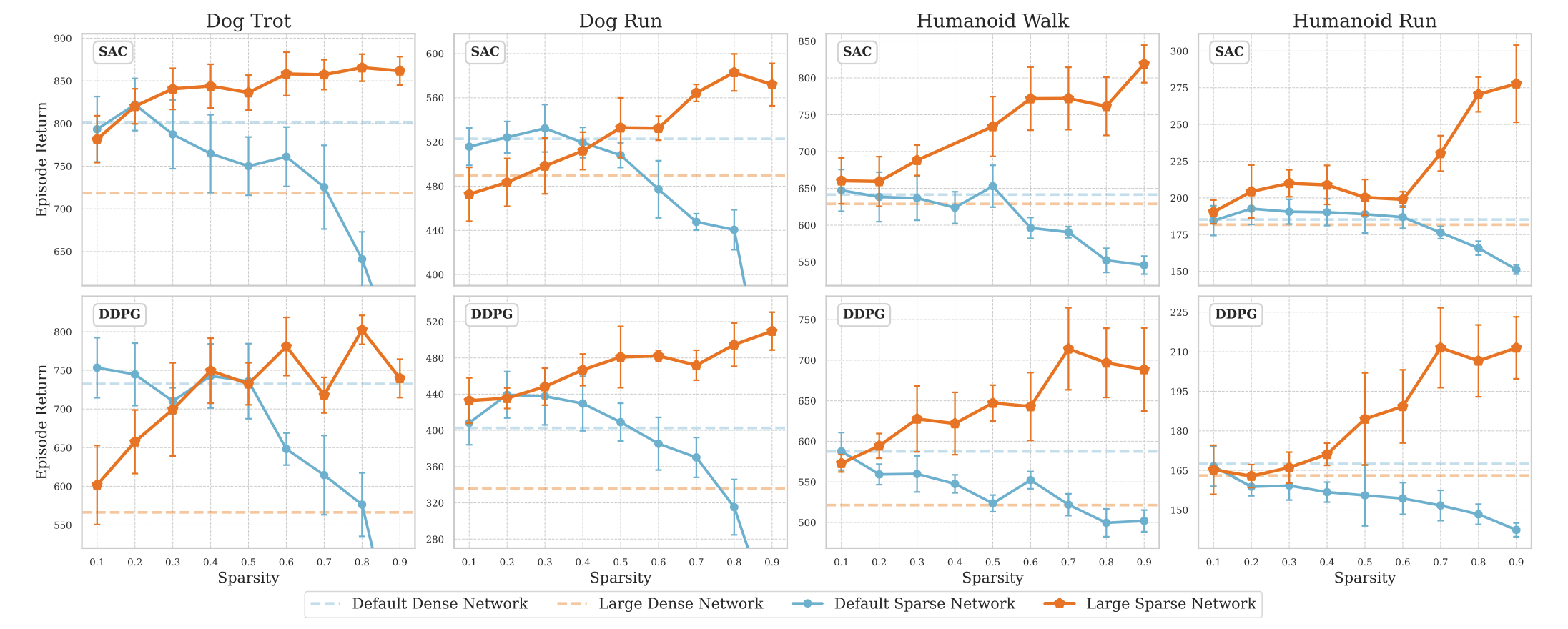
一般规模 (4.5M) 和大规模 (109M) 的稀疏网络对比

从这个图可以看出:

  • 一般规模的网络在高稀疏化后表现不佳, 这很可能是因为稀疏化导致了网络容量的显著下降, 使得模型无法捕捉到足够的环境信息.
  • 当网络规模增大时, 只允许学习一部分参数的高稀疏性的网络几乎总是优于原网络, 且此时比具有相同可学习参数量的稠密网络有更好的性能.

One-Shot 随机剪枝

关于如何控制稀疏性, 论文采用了通过一次随机剪枝进行静态稀疏训练的方式. 在初始化时为每一层 $l$ 生成二进制掩码 $M^l \in \{0, 1\}^{n^l \times n^{l-1}}$, 训练过程中有效权重计算为 $W = M \odot W$, 其中 $\odot$ 表示 Hadamard 乘积. $M$ 在训练过程中保持不变.

随机剪枝的方式非常简单, 只需要确定每一层的稀疏率 $s^l$:

  • 均匀分布: 每一层的稀疏率 $s^l$ 都是相同的, 即 $s^l = s$.
  • Erdos-Renyi: 对于全连接层, 取 $s^l = 1-\frac{n^l+n^{l-1}}{n^l n^{l-1}}$; 对于有 $w^l \times h^l$ 卷积核的卷积层, 取 $s^l = 1-\frac{n^l+n^{l-1}+w^l+h^l}{n^l n^{l-1} w^l h^l}$.

参数壁垒和稀疏化

实验显然带来了一个疑问: 稀疏网络在参数较少的情况下, 是如何实现优于密集网络的性能的?

表达能力

论文用 稳定秩 (Stable rank, Srank) 来衡量网络的表达能力. 具体来说:

$$ \mathrm{Srank}(W) = \sum_{j=1}^m \mathbb{I}(\sigma_j(W) > \tau) $$

其中 $W$ 是网络的权重矩阵, $\sigma_j(W)$ 是 $W$ 的第 $j$ 个奇异值, $\tau$ 是一个阈值.

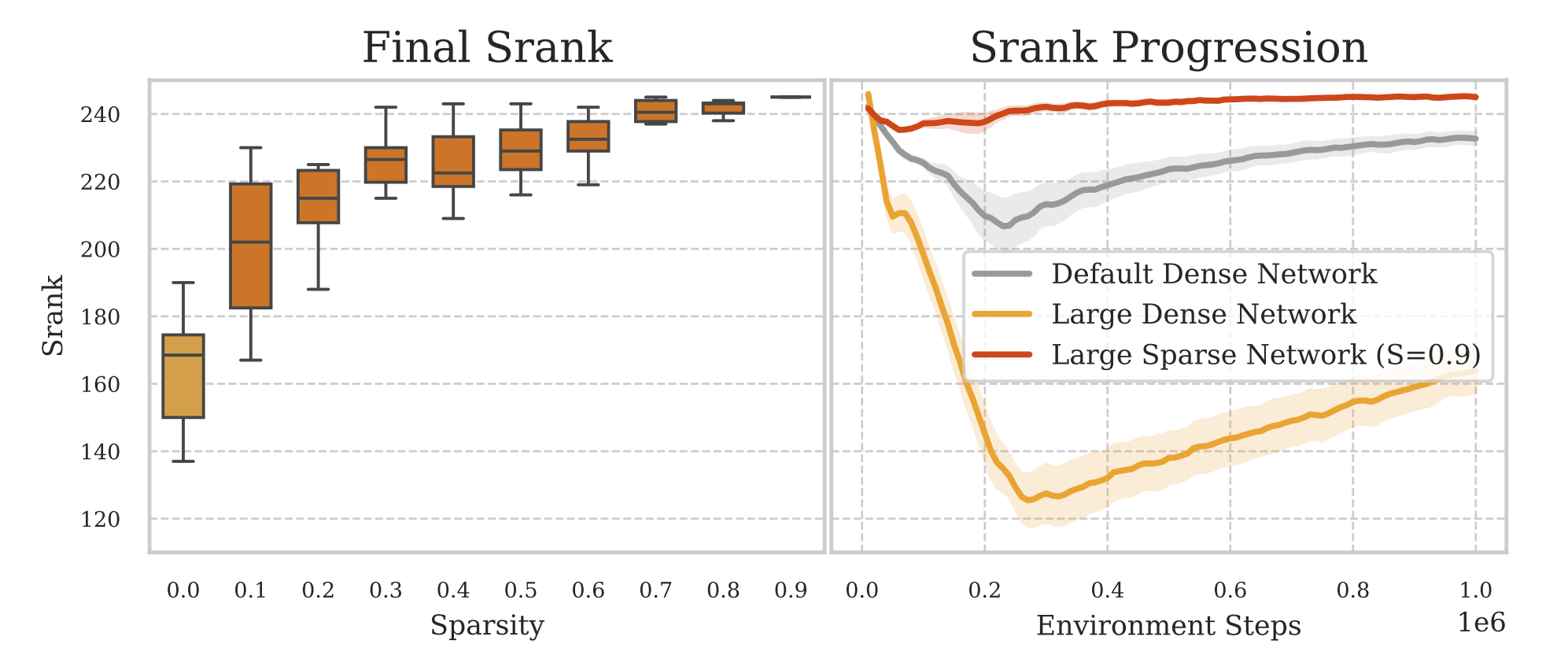
不同网络的 Srank

从这个图可以看出:

  • 提高网络的稀疏性会导致 Srank 的一致提升, 逐渐接近理论上限.
  • 对于稠密网络, 扩大网络规模会导致 Srank 的显著下降, 这可能是 DRL 中的规模壁垒的原因.

可塑性

有研究表明 DRL 网络的病态症状 (pathological symptoms) 与网络的可塑性 (plasticity) 下降有关 . 论文采用两个指标来衡量网络的可塑性:

  • 静默比率 (Dormant Ratio) : 衡量网络中静默神经元的比例. 层 $\ell$ 中的第 $i$ 个神经元的静默分数 $\rho_i^{\ell}$ 可以定义为: $$ \rho_i^{\ell} = \frac{\mathbb{E}_{x \sim P(\cdot; D)} | h_i^{\ell}(x)|}{\frac{1}{H^\ell} \sum_{k \in h} \mathbb{E}_{x \sim P(\cdot; D)} | h_k^{\ell}(x)|} $$ $h(x)$ 表示神经元激活, $H^{\ell}$ 表示第 $\ell$ 层神经元的数量. 如果 $\rho_i^{\ell} < \tau$, 则认为该神经元是静默的.
  • 梯度范数 (Gradient Norm) : 衡量网络中神经元的梯度 L2 范数. 如果梯度范数很小, 很可能意味着网络失去了学习能力.

不同网络的可塑性

正则化

论文认为稀疏性网络隐含了一种正则化机制.

  • 参数范数 (Parameter Norm) : 衡量网络中参数的 L2 范数. 参数如果出现持续的无界增长通常是病态的. 实验表明, 大型稀疏网络的参数范数与具有同等可学习参数的小型密集网络相当甚至更低.
  • 简单性偏差 (Simplicity Bias) : 神经网络倾向于学习简单的模式. 实验表明, 稀疏网络的简单性偏差分数更高, 促进更简单的解决方案.

梯度干扰

梯度干扰 (Gradient Interference) 指不同的数据集之间的梯度相互干扰, 使得模型难以学习. 具体来说, 对于 $k$ 个训练样本 $x_1, x_2, \ldots, x_k$, 梯度干扰矩阵 $C_k \in \mathbb{R}^{k \times k}$ 可以定义为:

$$ C_k[i, j] = \frac{\langle \nabla_{\theta} \ell(x_i, \theta), \nabla_{\theta} \ell(x_j, \theta) \rangle}{\|\nabla_{\theta} \ell(x_i, \theta)\|_2 \|\nabla_{\theta} \ell(x_j, \theta)\|_2} $$

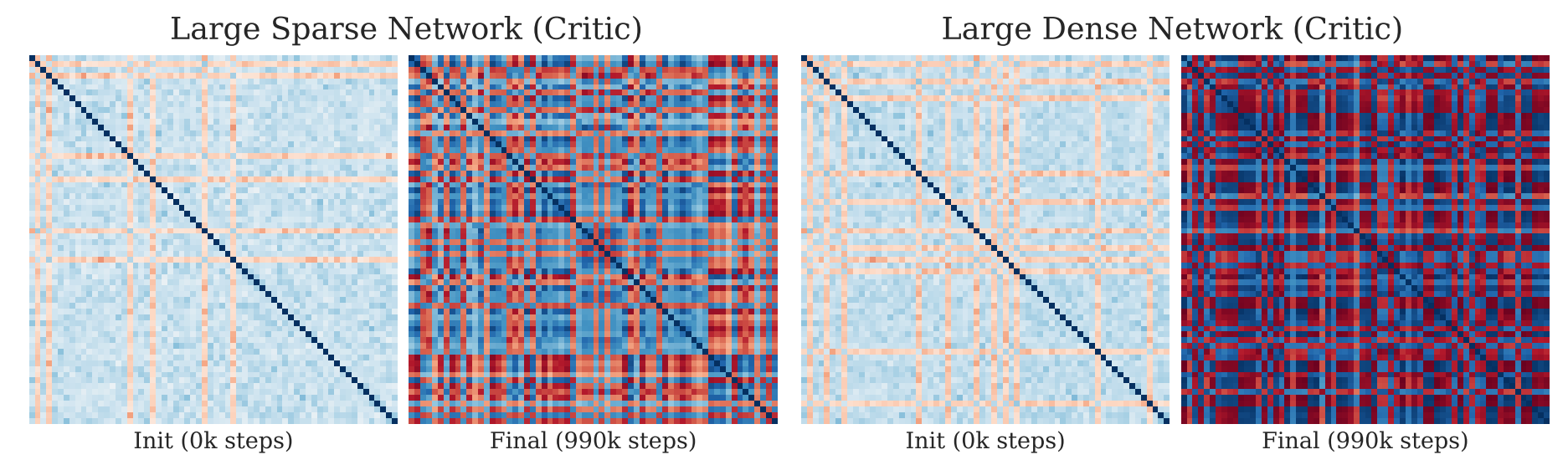
紧密与稀疏网络的梯度干扰

此热图中稀疏网路颜色更浅, 说明梯度干扰更小.

[Spotlight] 多视图去噪

MVC

现有的多视图聚类 (Multi-View Clustering, MVC) 算法在聚类性能上表现出色, 一般流程就是通过编码器提取表示, 采用特征融合策略, 最后用于下游聚类任务. 但现有的方法一般假设图像干净, 如果某些视图出现噪声, 会严重影响聚类性能, 甚至不如单视图.

论文 [] Unknown-material 提出了一个新的 自动识别和修正的多视图聚类 (Automatic Identification and Rectification Multi-View Clustering, AIRMVC) 框架, 与先前增加噪声容忍度或者优化结构的方法不同, AIRMVC 框架可以专门用于噪声数据识别和修正.

噪声识别

对于多视图数据集 $\{x^v\}_{v=1}^V$, 使用一个编码网络生成表示 $E^v = F^v(x^v; \Theta^v)$, 其中 $F^v$ 是第 $v$ 个视图的编码器. 随后先过一层 MLP, 然后用高斯混合模型 (Gaussian Mixture Model, GMM) (参看 机器学习基础) 建模分布.

$$p(E)=\sum_{k=1}^K \pi_k \mathcal{N}(E; \mu_k, \sigma_k)$$

其中 $\sum_{k=1}^K \pi_k = 1$ 是混合系数, 可以认为是某个隐变量 $q_i=k$ 的概率. 这里我们用网络的软预测 $p(y_i=k|x_i)$ 来代替. 根据 GMM 的 EM 算法, 可以更新 GMM 参数:

$$ \begin{aligned} \mu_k &= \mathrm{Norm} \left(\frac{\sum_{i=1}^N p(y_i=k|x_i) E_i}{\sum_{i=1}^N p(y_i=k|x_i)} \right)\\ \sigma_k &= \frac{\sum_{i=1}^N p(y_i=k|x_i) (E_i - \mu_k)(E_i - \mu_k)^\top }{\sum_{i=1}^N p(y_i=k|x_i)} \\ \end{aligned} $$

其中, $\mathrm{Norm}(\cdot)$ 是 $\ell_2$ 归一化 (疑惑: 归一化后计算 $\sigma_k$ 的时候不会受到影响吗?). 因此:

$$ \begin{aligned} \pi_{ik} &= p(q_i = k | x_i) \\ &= \frac{\exp \left(- \left(E_i - \mu_k \right)^\top \left(E_i - \mu_k \right) / 2\sigma_k \right)}{\sum_k \exp \left(- \left(E_i - \mu_k \right)^\top \left(E_i - \mu_k \right) / 2\sigma_k \right)} \\ &= \frac{\exp \left( E_i^\top \mu_k / \sigma_k \right)}{\sum_k \exp \left( E_i^\top \mu_k / \sigma_k \right)} \end{aligned} $$

$\pi_{ik}$ 就是样本分配给簇 $\mu_k$ 的软预测. 现在把噪声的识别问题转化为异常问题: 如果样本是无噪或低噪的, 其在不同视图中的软预测和簇分配应该保持一致.

引入一个二部 GMM 以自动识别给定样本的干净概率.

$$ p(y_i=q_i|x_i) = \pi_{y=q|i} = p(\pi_{y=q|i}, a=1) + p(\pi_{y=q|i}, a=0) $$

其中 $a=1$ 表示均值较高的干净样本簇, 而 $a=0$ 对应均值较低的样本簇 (什么意思?). 并把前者作为是干净样本的概率 $\phi_i$.

混合校正

检测样本噪声概率后, 我们采用混合校正策略, 利用预测的软分布组合来进行噪声修正:

$$ \begin{aligned} y_i^v &= h(E_i^v) \\ m_i^v &= \phi_i^v y_i^v + (1 - \phi_i^v) y_i^1 \end{aligned} $$

这里我们基于的假设是第一个视图总是干净的. 显然, 如果图像噪声越大, 越倾向于使用第一个视图的预测.

由此给出修正损失 (rectification loss), 即直接预测的损失与修正后的损失之间的交叉熵:

$$ \mathcal{L}_{\mathrm{rs}}=\frac{1}{V-1} \sum_{v=2}^V \left( -\sum_{i=1}^N \sum_{j=1}^K m_{ij}^v \log y_{ij}^v \right) $$

抗噪对比

使用对比学习的方法. 用 $s(E_i^m, E_j^n)$ 表示样本 $i$ 和 $j$ 在视图 $m$ 和 $n$ 中的相似度. 引入二者的鲁棒对比损失:

$$ \ell^{mn} = \mathbb{I}\{ (y_i^m)^\top (y_j^n) \ge \tau \} \left( \log (1 - s(E_i^m, E_j^n)) + \log (1-s(E_j^m, E_i^n)) \right) $$

$\tau$ 是通过选择相似样本来控制对比学习中样本对构建的置信阈值.

则视图的噪声鲁棒对比损失 (noise-robust contrastive loss) 损失为:

$$ \mathcal{L}_{\mathrm{con}} = \frac{1}{V(V-1)} \sum_{m=1}^V \sum_{n=1, n \ne m}^V \ell^{mn} $$

目标函数

我们再加入一个重建损失 (reconstruction loss) 来让编码器更好地学习特征:

$$ \mathcal{L}_{\mathrm{rec}} = \sum_{v=1}^V \sum_{i=1}^N \| x_i^v - G^v(F^v(x_i^v; \Theta^v); \Phi_i^v) \|_2^2 $$

$G$ 是解码器. 最终定义损失为:

$$ \mathcal{L} = \mathcal{L}_{\mathrm{rs}} + \alpha \mathcal{L}_{\mathrm{con}} + \beta \mathcal{L}_{\mathrm{rec}} $$

AIRMVC

算法AIRMVC

输入 > $N$ 个视图数据集 $\{x^v\}_{v=1}^V$.

输出 > 聚类标签 $R$.

  1. 计算 GMM 中 $\mu_k, \sigma_k$ 和干净样本概率 $\phi_i$ (E 步).
  2. 利用编码器 $F$ 计算样本表示 $E^v = F^v(x^v; \Theta^v)$.
  3. 识别并纠正其中的噪声样本, 同时计算噪声修正损失 $\mathcal{L}_{\mathrm{rs}}$.
  4. 计算噪声鲁棒对比损失 $\mathcal{L}_{\mathrm{con}}$ 和 重建损失 $\mathcal{L}_{\mathrm{rec}}$, 得出总损失 $\mathcal{L}$.
  5. 利用 $\mathcal{L}$ 反向传播更新模型.
  6. 重复步骤 1-5 直到收敛.
  7. 最后, 对每个样本 $i$, 计算其在 GMM 中的最大概率簇分配, 得到聚类标签 $R_i = \argmax_k p(y_i=k|x_i)$.

AIRMVC

[Spotlight] 生成图像对齐

现在 AI 生成的图像已经高度逼真, 以至可以用来作为训练数据. 但直接将生成图像作为真实图像用于训练, 会导致由于真实域和合成域模态差异而引发的模态崩溃. 论文 [] Unknown-material 提出了一个新的 生成图像学习模态对齐方法 (Generative Modality Alignment for generated Image Learning, GMAIL), 将生成的图像视为一种独立的模态, 并将其与同一隐藏空间中的真实图像对齐.

算法GMAIL

输入 > 真实图像数据集 $\mathcal{D}_R$, 生成图像数据集 $\mathcal{D}_G$.

输出 > 对齐后的 VLM.

参考文献

  • Kumar, A., Agarwal, R., Ghosh, D., and Levine, S. Implicit under-parameterization inhibits data-efficient deep reinforcement learning. In International Conference on Learning Representations, 2021.
  • Nikishin, E., Schwarzer, M., D’Oro, P., Bacon, P.-L., and Courville, A. The primacy bias in deep reinforcement learning. In International conference on machine learning, pp. 16828–16847. PMLR, 2022.
  • Sokar, G., Agarwal, R., Castro, P. S., and Evci, U. The dormant neuron phenomenon in deep reinforcement learning. In International Conference on Machine Learning, pp. 32145–32168. PMLR, 2023.
  • Abbas, Z., Zhao, R., Modayil, J., White, A., and Machado, M. C. Loss of plasticity in continual deep reinforcement learning. In Conference on Lifelong Learning Agents, pp.620–636. PMLR, 2023.
  • Lyle, C., Zheng, Z., Khetarpal, K., van Hasselt, H., Pascanu, R., Martens, J., and Dabney, W. Disentangling the causes of plasticity loss in neural networks. arXiv preprint arXiv:2402.18762, 2024b.
  • Shah, H., Tamuly, K., Raghunathan, A., Jain, P., and Netrapalli, P. The pitfalls of simplicity bias in neural networks. Advances in Neural Information Processing Systems, 33: 9573–9585, 2020.
本文遵循 CC BY-NC-SA 4.0 协议
© 2025 LeoDreamer
使用 Hugo 构建