传统 TTA 方法
野外测试时自适应 (Wild Test-Time Adaptation, WTTA) 相较于温和的 TTA, 需要在数据极其稀少时让模型适应从未见到过的领域, 通常有三个实际挑战:
- 有限的数据流. 批大小通常为 $1$.
- 测试域是混合的分布. 通常由 $k$ 个子域组成: $D_{\text{test}} = \sum_{i=1}^k \Pi_i \cdot D_i$, 其中 $\Pi_i$ 是每个子域的混合系数.
- 标签的不平衡性和浮动性. 测试标签分布不均, 且可能会随着时间的推移而变化.
常见的 TTA 方法是熵最小化策略 (这篇博客 有提及, 如 Tent 方法), 但当 TTA 的环境从 mild 变为 wild 时, 熵最小化的效果会大打折扣, 因此一些现有的工作是做样本过滤筛选, 例如 SAR 和 DeYO .
局部不一致性
为此, 论文 [] Unknown-material 提出了一个对模型输出确定性的替代方案, 即区域置信度.
熵最小化的核心思想是通过引导预测概率向主要的类别集中收敛, 其有效性很大程度上依赖于局部一致性, 也就是附近的点应该有相似的预测概率. WTTA 中, 局部不一致现象非常普遍, 此时简单的熵最小化会导致性能崩溃.
在此基础上, 必须解决优化方向与区域目标之间的偏差, 并减少局部区域内不一致预测概率的方差.
定义
考虑样本 $x$ 和其一个局部区域 $\Omega$, $x$ 在 $\Omega$ 上的 区域置信度 (Region Confidence) 定义为在 $\Omega$ 上熵损失的积分 (偏差项) 加上 $x$ 的预测概率与 $\Omega$ 中样本预测概率的 KL 散度 (方差项):
$$ \mathcal{L}_{\text{RC}}(x) = - \int_{\Omega} \sum_{i=1}^C p_{\theta}(\hat{x})_i \log p_{\theta}(\hat{x})_i d\hat{x} + \lambda \int_{\Omega} D_{KL}(p_{\theta}(\hat{x}) \| p_{\theta}(x)) d\hat{x} $$这里我们采用积分, 意味着理论可以在无限样本上整合损失项.
ReCAP
然而, 区域置信度的计算相当困难. 首先 $\Omega$ 的范围选择不确定, 其次两项都不能直接计算, 需要大量近似采样和前向传播的步骤. 为了降低训练复杂度, 论文引入了一种新的 区域置信度自适应代理 (Region Confidence Adaptation Proxy, ReCAP) 框架.
概率区域
我们先确定 $\Omega$ 的范围. 我们从主干网络的隐藏层中找区域置信度, 具体来说, 我们选定一个隐藏层, 输入 $x$ 后计算 $x$ 在经过网络中此隐藏层之后的特征 $z$, 然后对 $z$ 做一个仿射变换, 得到一个分类器的输出概率:
$$ p_{\theta}(z)_i = (\text{softmax}(Az+b))_i $$下标 $i$ 表示第 $i$ 个类别, $A$ 和 $b$ 是分类器线性层的参数.
关于局部区域, 我们将其建模成一个多元高斯分布, 而非静态区域:
$$ \Omega(z_t) := \mathcal{N}(z_t, \tau \cdot \Sigma) $$其中, $\Omega(z_t)$ 是第 $t$ 个测试批次 $z_t$ 的局部区域, 它是以 $z_T$ 为中心的高斯区域. $\Sigma$ 是基于少量源数据得到的方差对角矩阵, $\tau$ 是一个超参数, 用于控制范围.
置信度度量
接下来我们给出一个估计置信度的高效度量, 在此省略论文的数学推导, 直接给出结果:
定理偏差项的有效度量
给定一个特征 $z$ 及其局部区域 $\Omega$, 该局部区域服从高斯分布 $\mathcal{N}(z, \Sigma)$. 整个分布上的熵损失期望具有上界:
$$ \begin{aligned} &\mathbb{E}[\mathcal{L}_{\text{ent}}] = -\mathbb{E}_{\hat{z} \sim \mathcal{N}(\mu, \Sigma)} \sum_{i=1}^C p_{\theta}(\hat{z})_i \log p_{\theta}(\hat{z})_i \\ &\le \sum_{j=1}^C \frac{e^{u_j}}{\sum_{k=1}^C e^{u_k}} \log \sum_{i=1}^C e^{u_i - u_j} \triangleq \mathcal{L}_{\text{RE}}(z) \end{aligned} $$其中 $u_j = a_j \cdot z + b_j + \frac{1}{2} a_j \Sigma a_j^T$.
定理方差项的有效度量
给定一个特征 $z$ 及其局部区域 $\Omega$, 该局部区域服从高斯分布 $\mathcal{N}(z, \Sigma)$. 此分布输出概率与中心概率之间的 KL散度的期望值具有上界：
$$ \begin{aligned} &\mathbb{E}[D_{KL}(p_{\theta}(\hat{z}) \| p_{\theta}(z))] \\ &\le \sum_{j=1}^C \frac{e^{v_j}}{\sum_{k=1}^C e^{v_k}} \log \sum_{i=1}^C \frac{e^{v_j}}{\sum_{k=1}^C e^{v_k}} e^{\frac{1}{2} (a_i-a_j) \Sigma (a_i-a_j)^T} \triangleq \mathcal{L}_{\text{RI}}(z) \end{aligned} $$其中 $v_j = a_j \cdot z + b_j$.
因此我们只需要最小化不等式右侧的代理 $\mathcal{L}_{\text{RE}}(z)$ 和 $\mathcal{L}_{\text{RI}}(z)$ 就可以了, 这个计算难度非常低, 不需要额外的采样和前向传播.
ReCAP 训练
我们也做样本过滤, 但是我们现在使用区域熵 $\mathcal{L}_{\text{RE}}$ 来识别可靠的样本, 并在适应过程中优化, 具体来说就是:
$$\min_{\theta}\frac{\mathbb{I}_{\{\mathcal{L}_{\text{RE}}(x)<\tau_{\text{RE}}\}}(\mathcal{L}_{\text{RE}}(x)+\lambda\mathcal{L}_{\text{RI}}(x))}{\exp(\mathcal{L}_{\text{RE}}(x)-\mathcal{L}_0)}$$分母表示加权项, $\tau_{\text{RE}}$ 表示区域熵的阈值, $\mathcal{L}_0$ 是超参数.
实验与可视化
实验表明, ReCAP 能较好地应对数据稀缺和标签不平衡的情况, 而且还可以和之前基于熵最小化的方法 (如 SAR 和 DeYO) 结合, 进一步提升性能, 且算法开销很低.
两个超参数 $\tau$ 和 $\lambda$ 分别控制区域范围和方差项的权重, 论文取 $\tau = 1.2 \in [0.5, 1.5], \lambda = 0.5$, 实际上模型对两个参数也具有相对较好的鲁棒性.
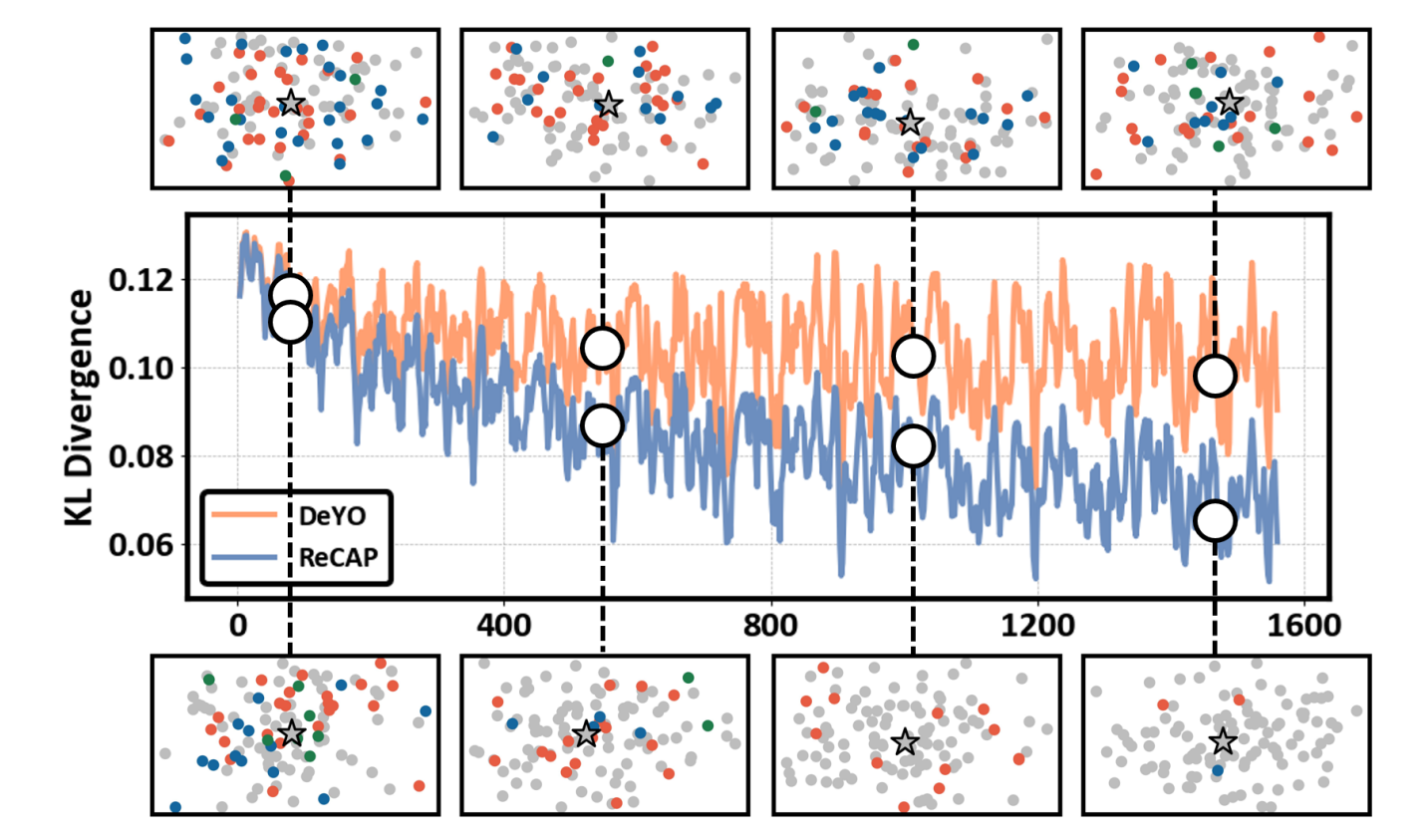
由于引入了区域置信度, 分类的区域一致性确实得到了改善, 下图中的不同颜色表示此区域内分类不同的类别, 可以看到随着迭代, 分类区域的颜色变得越来越一致, 这也说明了区域置信度的有效性.
参考文献
- Niu, S., Wu, J., Zhang, Y., Wen, Z., Chen, Y., Zhao, P., and Tan, M. Towards stable test-time adaptation in dynamic wild world. In Internetional Conference on Learning Representations, 2023
- Lee, J., Jung, D., Lee, S., Park, J., Shin, J., Hwang, U., and Yoon, S. Entropy is not enough for test-time adaptation: From the perspective of disentangled factors. In The Twelfth International Conference on Learning Representations, 2024.