论文阅读 - 运动结构恢复

3D 重建主要指估计一组图像中场景的 3D 属性的问题.

通常的 运动结构恢复 (Structure from Motion, SfM) 问题是给定一组图像, 恢复相机的姿态和场景的 3D 点云. 一般步骤如下:

特征匹配: 通过在两幅或多幅图像中找到相同的特征点 (例如, 使用 SIFT 或 ORB 算法), 确定这些特征点的匹配关系.
相机位姿估计: 使用两个或更多的图像及其对应的特征点, 估计相机的外参 (即相机位置和朝向). 这里一般有增量式 (从两幅图像开始, 逐步添加更多图像) 和全局式 (一次性处理所有图像) 两类方法.
三角化: 用于恢复三维点的位置. 基本原理是通过已知的相机视角和匹配点的位置, 利用几何约束来计算三维点的空间坐标. 常见的方法是直接线性变换 (Direct Linear Transform, DLT) 或基于光束平差法 (Bundle Adjustment, BA) 的非线性优化方法.
三维点恢复: 通过三角化得到的三维点通常会是一个稀疏点云, 代表了场景中关键特征的空间位置. 对于每个匹配的特征点, 三角化将其映射到三维空间中的位置.

增量式 SfM 的典型结构

介绍几个 3D CV 概念.

定义 相机的 投影矩阵 (Projection Matrix) $P_i \in \mathbb{R}^{3 \times 4}$ 用于将 3D 点投影到 2D 图像平面, 包含 外参 $g_i \in \mathbb{SE}(3)$ 和 内参 $K_i \in \mathbb{R}^{3 \times 3}$. $$ g = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix}, \quad K = \begin{bmatrix} f & 0 & p_x \\ 0 & f & p_y \\ 0 & 0 & 1 \end{bmatrix} $$ 其中 $R$ 是旋转阵, $t$ 是平移量, $f$ 是焦距, $(p_x, p_y)$ 是主点坐标, 一般取图像中心.

定义 两个相机之间的 本质矩阵 (Essential Matrix) $E \in \mathbb{R}^{3 \times 3}$ 用于关联两幅图像中 归一化相机坐标 的对应点 $x_1, x_2 \in \mathbb{R}^3$: $$ x_2^T E x_1 = 0 $$其中 $x_1, x_2$ 是归一化的相机坐标, 即 $x_i = K_i^{-1} p_i$, $p_i$ 是图像平面上的点坐标.

可以证明本质矩阵 $E = t \times R$, 其奇异值满足 $\sigma_1 = \sigma_2 \gt 0, \sigma_3 = 0$, 其自由度是 $5$, 需要注意求解本质矩阵需要事先知道两个相机的内参, 最常用的方法是八点算法 (Eight-Point Algorithm).

定义 两个相机之间的 基础矩阵 (Fundamental Matrix) $F \in \mathbb{R}^{3 \times 3}$ 用于关联两幅图像中 像素坐标 的对应点 $p_1, p_2 \in \mathbb{R}^2$: $$ p_2^T F p_1 = 0 $$

基础矩阵隐含了内参的不确定性, 因此其自由度是 $7$. 求解基础矩阵不需要知道相机的内参, 但需要知道点的对应关系.

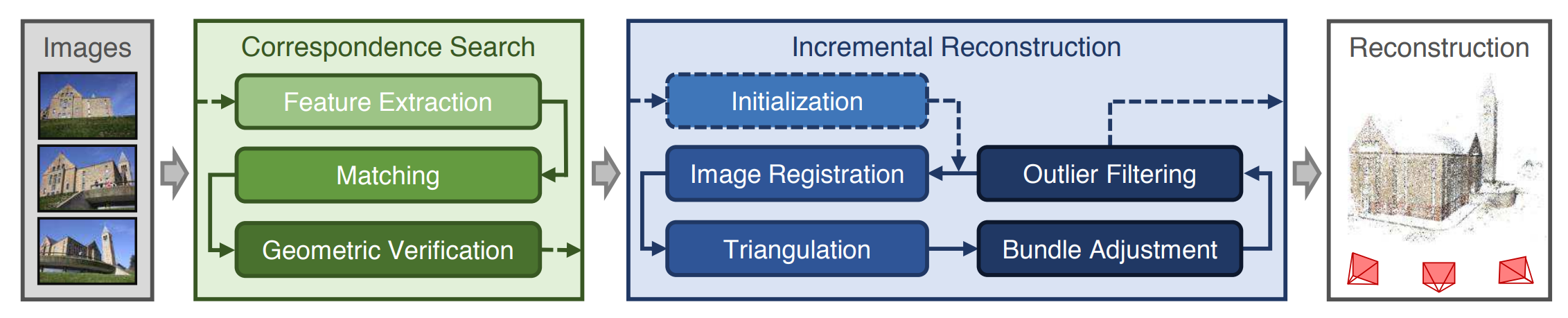
COLMAP (CVPR 2016)

COLMAP 是一个开山级别的开源的 SfM 框架, 由 Johannes L. Schönberger 和 Jan-Michael Frahm 在 2016 年提出 [] Unknown-material . 它提供了一个完整的增量式 SfM 流程, 包括特征提取、匹配、相机姿态估计、三角化和稠密重建等步骤.

COLMAP 没有改变 SfM 的流程, 但它引入了几个大量的优化来应对 SfM 常见的挑战.

场景图增强

在特征匹配时, 每次要选取一对图片, COLMAP 针对图像选取做了改进.

算法COLMAP-图像选取 输入 > 一组图像对. 输出 > 筛选出的图像对. 首先估计一对图像的 基础矩阵. 如果找到的内点数 $\ge N_F$, 就认为这对图像在几何上是验证通过的. 然后估计 单应矩阵, 并统计其内点数 $N_H$. 如果比例 $N_H/N_F < \epsilon_{HF}$, 则判定为一般场景下的运动相机, 而不是退化的纯旋转或平面情况. 如果相机已标定, 还会估计 本质矩阵, 并统计内点数 $N_E$. 若比例 $N_E/N_F > \epsilon_{EF}$, 说明相机内参标定是正确的. 在满足如上条件时, 分解本质矩阵, 通过内点对应三角化点, 并计算三角化角度 $\alpha_m$, 以此区分是纯旋转还是平面场景. 互联网照片中可能由于水印、时间戳等等导致伪匹配 (WTF), 此时通过估计相似变换并检测是否集中在图像边缘来识别. 如果边缘内点比例超过阈值, 则认为是 WTF 匹配, 将其剔除.

需要注意, 筛选完后在场景图中标注其模型类型, 并保留支持度最高的模型的内点 (即 $N_H/N_E/N_F$) 信息.

下一个最佳视角选择

既然是增量式的, 每次都要加一张新的图像, 选取非常重要, 因为每一次决策都会影响剩下的整个重建过程. 一种常见的策略是选择能看到最多已三角化点的图像. 不过 COLMAP 还考虑了这些点分布的均匀性.

首先将图像划分为网格, 每个格子都是空的. 当某个三维点 第一次 落入一个空格子时，该格子变为满，并增加该图像的得分 $S_i$. 显然这种方法更倾向于选择分布均匀的图像.

点太少时可能无法反映分布情况. 此时扩展为一个多分辨率金字塔, 在不同分辨率下重复划分并加权累积得分, 以求结果更稳健.

鲁棒高效三角化

怎么在大量外点中找到轨迹是难题之一, COLMAP 把此建模为 RANSAC 问题.

算法COLMAP-三角化 输入 > 特征轨迹 $T = \{T_n \mid n = 1, \cdots, N_T \}$, 每个观测 $T_n$ 包含归一化图像点 $\bar{x}_n \in \mathbb{R}^2$ 和相机为位姿 $P_n \in SE(3)$. 输出 > 轨迹中找到一个最大的一致集, 符合两个视图三角化结果. 随机选择两观测 $(a,b)$, 得到三角化点 $X_{ab} \sim \tau \left( \bar{x}_a, \bar{x}_b, P_a, P_b \right)$, 特别地这里用 DLT 进行两视图三角化. 检查约束条件: 三角化角度必须大于 $\alpha$, 深度均为正, 且重投影误差小于 $t$. 将满足条件的观测放在一致集中. 用 RANSAC 迭代最大化一致集规模. 找到一个一致集后, 把它从轨迹中剔除. 随后递归, 直到再找一致集规模 <3 为止.

光束平差

传统的 BA 方法计算代价高, 且对外点敏感. 因此 COLMAP 做了如下优化:

在每次注册新图像后, 只对与该图像共享点的相机进行局部 BA, 避免在模型过大时频繁运行全局优化. 然后在适当的时机触发一次全局 BA，以消除累积误差.
在 BA 之后，重新进行三角化与外点检测. 先前因基线过小无法可靠三角化的点, 可能在新的相机加入后变得可观测, 这时就可以重新三角化. 若发现某些点重投影误差大于阈值, 就把它们从结构里移除.

冗余视角挖掘

互联网数据集有大量冗余照片, 没有显著提升, 但是却增加了 BA 计算成本. 然而 COLMAP 不是丢弃冗余图像, 而是将它们转化为低代价的约束.

对于给定的 $N_X$ 个点, 每张图可以用0-1可见向量 $v_i$ 表示. $a,b$ 之间的相似度可写为 $$V_{ab} = \| v_a \wedge v_b \| / \| v_a \vee v_b \|$$
在更新时, 如果图像是新添加的, 或者超过 $\epsilon_r$ 比例的观测值的重投影误差大于 $r$ 像素, 则认为它是受到影响的.
对于被影响的图像独立分组, 以便进行单独优化.
把未受影响的图像, 我们要划分为若干个组 $\mathcal{G}=\{ G_1, G_2, \ldots, G_k \}$, $G_i$ 中高度冗余, 把它们参数化为以一个单一的相机.
为此, 首先按照 $\|v_i\|$ 降序排列成 $\bar{I}$. 移除$\bar{I}$ 中第一个图像 $I_a$, 来找 $I_b$ 使得 $V_{ab}$ 最大.
如果 $V_{ab} > V$ 且 $|G_r| < S$, 则将图像 $I_b$ 从 \bar{I} 中移除并添加到组 $G_r$ 中, 否则创建一个新组, 如此往复.

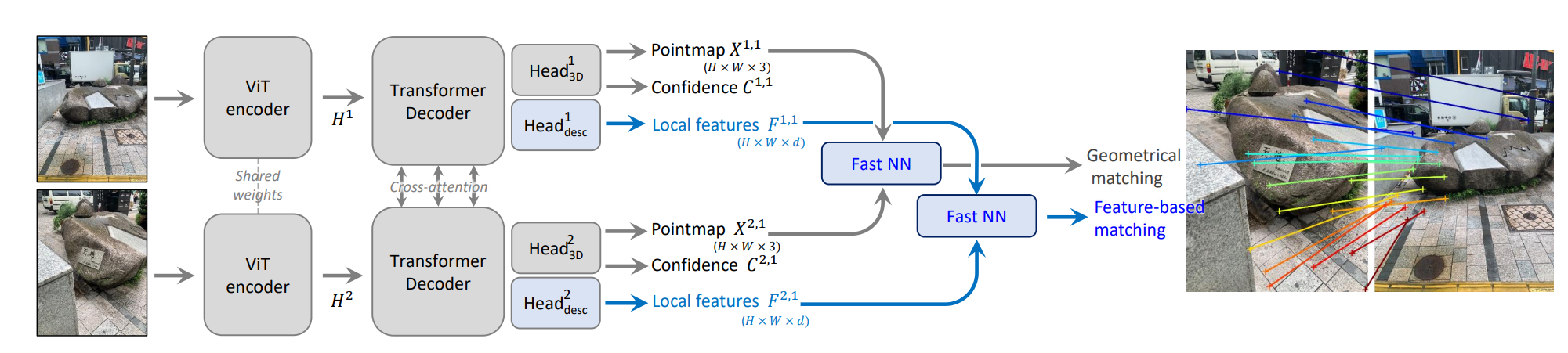
DUSt3R (CVPR 2024)

论文 [] Unknown-material 提出了一个新的 密集无约束立体 3D 重建 (Dense and Unconstrained Stereo 3D Reconstruction, DUSt3R) 模型, 该模型基于视觉几何学的原理, 通过深度学习方法简化了 3D 重建任务.

算法DUSt3R 输入 > 2 张 RGB 图像 $I^1, I^2 \in \mathbb{R}^{W \times H \times 3}$. 输出 > 对应的点图 $X^{1,1}, X^{2,1} \in \mathbb{R}^{W \times H \times 3}$ 和关联的置信度 $C^{1,1}, C^{2,1} \in \mathbb{R}^{W \times H}$. $X^{n,m}$ 表示相机 $n$ 的点图 $X^n$ 在相机 $m$ 的坐标系下的表示: $$ X^{n,m} = P_m P_n^{-1} h(X^n) $$其中 $P_n$ 是相机 $n$ 的投影矩阵, $h: (x,y,z) \to (x,y,z,1)$ 是齐次坐标变换. 也就是说二者都以相同的坐标系 $I_1$ 为参考. 两个输入图像首先通过共享权重的 Siamese ViT 编码器 进行编码, 生成两个 token 表示 $F^1, F^2$. $$ F^1 = \text{Encode}(I^1), \quad F^2 = \text{Encode}(I^2) $$ 在解码器联合推理. 每个解码器块会依次执行自我注意力和交叉注意力, 最后过传递给 MLP: $$ G_i^1 = \text{Decode}_i^1 \left(G_{i-1}^1, G_{i-1}^2 \right), \quad G_i^2 = \text{Decode}_i^2 \left(G_{i-1}^2, G_{i-1}^1 \right) $$ 最后用一个单独的回归头接受所有 token 并输出预测的点图和置信度: $$ X^{1,1}, C^{1,1} = \text{Head}^1 \left(G_0^1, \dots, G_B^1 \right), \quad X^{2,1}, C^{2,1} = \text{Head}^2 \left(G_0^2, \dots, G_B^2 \right) $$ 对于视图 $v \in \{1,2\}$ 和像素点 $i$, 其 3D 回归损失定义为: $$ \ell_{\mathrm{regr}}(v,i) = \left\| \frac{1}{z} X_i^{v,1} - \frac{1}{\bar{z}} \bar{X}_i^{v,1} \right\| $$ $z$ 用于归一化. 置信度损失定义为 3D 回归损失的加权平均: $$ \mathcal{L}_{\mathrm{conf}} = \sum_{v=1}^2 \sum_{i=1}^N C_i^{v,1} \ell_{\mathrm{regr}}(v,i) - \alpha \log C_i^{v,1} $$

然而, 这个网络每次只能处理一对图像. 因而论文 [] 引入一种后处理优化方法, 给定一组 $\{I^n\}_{n=1}^N$ 图像, 以图像为顶点建图, 连边表示共享一些内容, 可以通过置信度来计算二者的重叠, 然后过滤掉低置信度的配对.

现在如果要恢复所有相机的点图 $\{ \mathcal{X}^n \in \mathbb{R}^{W \times H \times 3} \}_{n=1}^N$, 则可以求解如下优化问题:

$$ \chi^* = \arg\min_{\chi, P, \sigma} \sum_{e=(n,m) \in \mathcal{E}} \sum_{v \in \{n,m\}} \sum_{i=1}^{HW} C_i^{v,n} \left\| \chi_i^v - \sigma_e P_e X_i^{v,n} \right\|. $$

$\sigma_e \gt 0$ 是缩放, $P_e \in \mathbb{R}^{3 \times 4}$ 是姿态. 为避免 $\sigma_e=0$ 的平凡解, 要求 $\prod_{e} \sigma_e = 1$.

MASt3R (ECCV 2024)

论文 [] Unknown-material 指出 DUSt3R 匹配精度较低, 因而基于其提出了一个新的 匹配和立体 3D 重建 (Matching And Stereo 3D Reconstruction, MASt3R) 模型.

相较于 DUSt3R, MASt3R 主要更关心点匹配, 做了以下改进:

除了预测点图和置信度, 还加上额外两个头输出密集特征: $$ D^1 = \text{Head}^1_D(G_0^1, \dots, G_B^1), \quad D^2 = \text{Head}^2_D \left(G_0^2, \dots, G_B^2 \right) $$
对于真实对应的点 $\hat{\mathcal{M}}=\{(i,j) \mid \hat{X}_i^{1,1} = \hat{X}_j^{2,1}\}$, 计算匹配损失 (实质上是匹配的交叉熵损失): $$ \mathcal{L}_{\mathrm{match}} =- \sum_{(i,j) \in \hat{\mathcal{M}}} \log \frac{s_\tau(i,j)}{\sum_k s_\tau(k,j)} + \log \frac{s_\tau(i,j)}{\sum_k s_\tau(i,k)} $$ 这里 $s_\tau(i,j) = \exp\left( -\tau D_i^1 \cdot D_j^2 \right)$ 是点 $i$ 和 $j$ 的相似度, $\tau$ 是温度参数. 然你与置信度损失加权结合: $$ \mathcal{L}_{\mathrm{total}} = \mathcal{L}_{\mathrm{conf}} + \beta \mathcal{L}_{\mathrm{match}} $$
匹配两点的算法是让二者互为彼此的最近邻. 即: $$ \mathcal{M} = \{(i,j) \mid j = \argmin_{k} \|D_i^1 - D_k^2\|, i = \argmin_{k} \|D_j^2 - D_k^1\|\} $$ 直接枚举匹配的复杂度是 $\mathcal{O}(W^2H^2)$. 论文采用了一种迭代的策略, 即对每个点每次在图中找最近邻再映射到另一个图中, 直到收敛. 这样复杂度是 $\mathcal{O}(kWH)$.

MASt3R

对于更高分辨率的图像, 论文 [] 采用从粗到细匹配的策略.

算法MASt3R 高分辨率 输入 > 两张高分辨率 RGB 图像 $I_1, I_2 \in \mathbb{R}^{3 \times H \times W}$. 输出 > 对应的点图 $X^{1,1}, X^{2,1} \in \mathbb{R}^{W \times H \times 3}$ 和关联的置信度 $C^{1,1}, C^{2,1} \in \mathbb{R}^{W \times H}$. 做粗匹配, 下采样到适合匹配的分辨率 (512), 得到对应点集 $M_k^0$, $k$ 是下采样的数量. 对两个图像分别生成重叠的窗口裁剪 $W_1, W_2$, 每个窗口裁剪的最大维度固定为 512 像素, 并且相邻窗口之间有 50% 的重叠区域. 按照贪心算法枚举窗口对 $(w_1, w_2) \in W_1 \times W_2$, 使得覆盖 $M_k^0$ 的 90% 点对为止. 做细匹配, 对找出的每个窗口对用 MASt3R, 在局部图内找更精确的对应点. 把每个窗口的结果映射回原始坐标系, 并合并得到结果.

GLOMAP (ECCV 2024)

论文 [] Unknown-material 提出了一个全局的 SfM 方法, 直接进行联合全局三角化和相机位置估计. 问题建模为优化:

$$ \argmin_{X,c,d} \sum_{i,k} \rho \left( \|v_{ik} - d_{ik} (X_k-c_i) \| \right) $$

其中 $v_{ik}$ 是从相机 $c_i$ 观察点 $X_k$ 的全局旋转相机射线 (?? 应该是在图像中能计算得到的, 且要做归一化), $\rho$ 是 Huber 函数用于保持鲁棒性, 优化用 LM 优化器. 论文提出这个误差有界, 因此对噪声数据不敏感.

在处理图像时, 为保证图像相关性, 先做相机聚类:

计算每对图像可见点的数量, 构图为 $G$, 丢弃计数少于 $5$ 的图像对.
使用剩余图像对的中位数来设置内点阈值 $\tau$.
连接计数超过 $\tau$ 的图像对, 在 $G$ 中寻找连通分量来找到相机的良好约束群集.
递归地重复此过程, 每个连通分量作为单独的重建输出.

GLOMAP

VGGSfM (CVPR 2024)

论文 [] Unknown-material 基于常用的 SfM 框架, 提出了一个新的可以进行端到端训练的 视觉几何基础运动恢复结构 (Visual Geometry Grounded Structure from Motion) 模型.

算法VGGSfM 追踪器 输入 > 观察同一 3D 场景的 RGB 图像序列 $(I_i)_{i=1}^{N_I}, I_i \in \mathbb{R}^{3 \times H \times W}$, 给定的查询点 $y_i$. 输出 > 该点在图像 $I_j$ 的轨迹 $y_i^j$ 以及可见性 $v_i^j$. 先做特征提取, 用 4 个不同大小的 CNN 来计算帧 $I_i$ 的特征子图 $\{F_i^k\}_{k=1}^4$, 然后用双线性插值把它们上采样到相同大小, 随后拼接再卷积得到特征图 $F_i$. 对 $F_i$ 降采样 (每次做一次池化), 得到不同尺度下的特征张量金字塔. 将查询点扩展到所有帧中, 初始坐标都设为相同. 使用双线性采样从第一帧 (参考帧) 提取查询点的特征, 所有帧的初始特征都设为这个初始特征. 对每一个金字塔层级, 构造以每个查询点为中心的局部窗口, 并使用双线性插值采样局部特征, 随后与参考特征做内积衡量相似度, 得出相关性特征. 计算每个点相对于参考帧的相对位置 (即运动), 得出相对偏移编码特征. 把跟踪特征, 相对偏移编码特征和相关性特征拼接, 作为 Transformer 的输入. 通过 Transformer 更新坐标和特征, 直至收敛. 利用得到的追踪特征 $y_i^j$ 预测点的可见性 $v_i^j$. 同时引入 aleatoric 不确定性模型 来预测 $y_i^j$ 的方差 $\sigma_i^j$ (或者置信度), 我们假设 $\sigma_i^j$ 是对角的.

算法VGGSfM 输入 > 观察同一 3D 场景的 RGB 图像序列 $(I_i)_{i=1}^{N_I}, I_i \in \mathbb{R}^{3 \times H \times W}$. 输出 > 模型需要输出以下几点: 相机投影矩阵 $P_i \in \mathbb{R}^{3 \times 4}$. 点云 $X=\{x^i\}_{i=1}^M$, 其中 $x^i \in \mathbb{R}^3$ 是场景中每个点的三维坐标. 即此时对于 3D 点 $x^j$, 其在第 $i$ 个相机的 2D 投影为: $$ y_i^j = P_i (x^j) = \lambda K_i g_i x^j $$ 利用追踪器获得轨迹 $\mathcal{T} = \{T_i\}_{i=1}^{N_I}$, 其中 $T_i = \{y_i^j\}_{j=1}^{N_T}$ 是第 $i$ 个图像中查询点的轨迹, $N_T$ 是查询点的数量. 为了初始化相机 $\hat{P}$, 采用一个深度 Transformer 网络 $\mathbf{T}_P$: $$ \hat{P} = \mathbf{T}_{P}(\{\phi(I_i) \mid I_i \in \mathcal{I}\}, \{d^P(y_i^j) \mid \forall T_i \in \mathcal{T}, \forall y_i^j \in T_i\}). $$ $\phi(I_i)$ 表示 $I_i$ 的特征, $d^P(y_i^j)$ 表示在 $y_i^j$ 处的描述符. 把全局图像特征作为 query, 把每个查询点的轨迹-描述符对作为 key-value 对, 这时每个场景有 $N_T$ 个 token. 把交叉注意力的输出拼接上估计的初始相机位置 (例如八点算法) 作为相机参数 Transformer 网络的输入. 为了初始化点云 $\hat{X}$, 在给定初始相机 $\hat{P}$ 后, 采用一个深度 Transformer 网络作为三角化器: $$ \hat{X} = \mathbf{T}_{X}(\{d^X(y_i^j) \mid \forall T_i \in \mathcal{T}, \forall y_i^j \in T_i\}). $$ $d^P(y_i^j)$ 表示在 $y_i^j$ 处的描述符和其在初始点云 $\bar{X}$ 中位置编码的拼接. $\bar{X}$ 是通过闭式多视图 DLT 三角化得到的. 在轨迹 $\mathcal{T}$, 初始化的相机 $\hat{P}$ 和点云 $\hat{X}$ 的基础上, 利用光束法平差最小化重投影误差: $$ X, P = \mathrm{BA}(\mathcal{T}, \hat{P}, \hat{X}) = \argmin_{X, P} \sum_{i=1}^{N_I} \sum_{j=1}^{N_T} v_i^j \| y_i^j - P_i x^j \| $$ 为了稳定, 误差项会过滤 $v$ 低的, 置信度低的和重投影误差过大的点. 使用 Levenberg-Marquardt 优化器进行迭代优化. 然而反向传播需要此式可微, 因而论文引用 Theseus 库, 该库利用隐函数定理通过嵌套优化循环反向传播通过深度网络. 损失函数定义为: $$ \mathcal{L}(f_{\theta}(\mathcal{I}), p^\ast, \mathcal{T}^\ast, X^\ast) = \sum_{j=1}^{N_T} |x^{\ast j} - x^j| + |x^{\ast j} - \hat{x}^j| + \sum_{i=1}^{N_I} e_P (P_i^\ast, P_i) + e_P (P_i^\ast, \hat{P}_i) - \lambda \sum_{i=1}^{N_I} \sum_{j=1}^{N_T} \log \mathcal{N}(y_i^{\ast j} | y_i^j, \sigma_i^j) $$ $e_P(P, P')$ 指相机参数 $P, P'$ 之间的 Huber 损失. $P$ 有 8 个自由度, 因此这里参数化为一个 8 维向量. 用 AdamW 优化器优化模型, 直至收敛.

Dense-SfM (CVPR 2025)

Dense-SfM

VGGT (CVPR 2025)

论文 [] Unknown-material 提出了一个新的 视觉几何基础 Transformer ( Visual Geometry Grounded Transformer) 模型.

算法VGGT 输入 > 观察同一 3D 场景的 RGB 图像序列 $(I_i)_{i=1}^N, I_i \in \mathbb{R}^{3 \times H \times W}$. 输出 > 模型需要输出以下几点: 相机参数 $g_i = \left[q_i,t_i,f_i\right] \in \mathbb{R}^9$: 分别表示旋转四元数 $q_i \in \mathbb{R}^4$, 平移向量 $t_i \in \mathbb{R}^3$, 视场角 $f_i \in \mathbb{R}^2$. 深度图 $D_i \in \mathbb{R}^{H \times W}$: 为每个像素位置关联一个从该相机视角观察到的深度值. 点图 $P_i \in \mathbb{R}^{3 \times H \times W}$: 为每个像素关联其在场景中对应的三维空间点坐标. 这些 3D 点都在第一个相机的坐标系下表示, 因此是跨视图不变的. 轨迹特征 $T_i \in \mathbb{R}^{C \times H \times W}$: 给定一个固定的查询点 $y_q$, 输出其在所有图像 $I_i$ 的 2D 点 $y_i \in \mathbb{R}^2$ 轨迹 $\mathcal{J}(y_q) = (y_i)_{i=1}^N$. 需要注意, 并非直接输出轨迹, 而是为每个图像生成一个 $C$ 维的密集特征网格 $T_i$, 这些特征图随后被一个独立的追踪模块, 通过 $y_q$ 和 $T_i$ 用来计算任意点的对应关系和轨迹. 采用 DINO 把图像 $I_k$ 划分成 $K$ 个 token 的 patches $t^I_k \in \mathbb{R}^{K \times C}$. 所有视图 patches 之并 $t^I$ 作为网络的输入. 转换成 token $t_i^I$ 后, 再拼接上一个额外的相机 token $t_i^g$ 和四个寄存器 token $t_i^R$ , 每个相机和寄存器的 token 是逐帧的, 然后把得到的结果传递给网络. 骨干网络为一个大型 Transformer 模型. 在 Transformer 中采用帧间注意力 (针对 $t_k^I$) 和全局注意力 (针对 $t^I$) 机制交替进行, 称为交替注意力机制 (Alternating-Attention, AA). 网络输出的结果舍弃寄存器 $\hat{t}_i^R$, 其余的 $\hat{t}_i^I$ 和 $\hat{t}_i^g$ 用于预测. 通过一个四个额外的自注意力层和线性层把 $\hat{t}_i^g$ 转换成 $\hat{g}_i$ 以预测相机参数. 把 $\hat{t}_i^I$ 通过 DPT 层 转换为密集特征图 $F_i \in \mathbb{R}^{C'' \times H \times W}$. 每个 $F_i$ 通过一个 $3\times 3$ 卷积层映射到相应的深度图 $D_i$ 和点图 $P_i$. 并为每个深度图和点图预测 aleatoric 不确定性 $\Sigma_i^D$ 和 $\Sigma_i^P$ . 从 $F_i$ 中提取 $T_i \in \mathbb{R}^{C \times H \times W}$, 并采用 CoTracker2 架构作为追踪轨迹模块 . 该模块接收查询点 $y_q$ 和特征图 $F_i$, 输出每个图像 $I_i$ 中查询点的 2D 位置 $\hat{y}_{j,i}$, 其中 $j$ 是查询点的索引. 使用 Huber 损失得出相机损失: $$ \mathcal{L}_{\mathrm{cam}} = \sum_{i=1}^N \left\| \hat{g}_i - g_i \right\|_{\epsilon} $$ 根据 aleatoric 不确定性, 加入梯度, 得出深度损失和点图损失: $$ \begin{aligned} \mathcal{L}_{\mathrm{depth}} &= \sum_{i=1}^N \left\| \Sigma_i^D \odot \left( \hat{D}_i - D_i \right) \right\| + \sum_{i=1}^N \left\| \Sigma_i^D \odot \left( \nabla \hat{D}_i - \nabla D_i \right) \right\| - \alpha \log \Sigma_i^D \\ \mathcal{L}_{\mathrm{point}} &= \sum_{i=1}^N \left\| \Sigma_i^P \odot \left( \hat{P}_i - P_i \right) \right\| + \sum_{i=1}^N \left\| \Sigma_i^P \odot \left( \nabla \hat{P}_i - \nabla P_i \right) \right\| - \alpha \log \Sigma_i^P \end{aligned} $$ 轨迹损失定义为: $$ \mathcal{L}_{\mathrm{track}} = \sum_{j=1}^M \sum_{i=1}^N \| y_{j,i} - \hat{y}_{j,i} \| $$ 最终的损失函数为: $$ \mathcal{L} = \mathcal{L}_{\mathrm{cam}} + \mathcal{L}_{\mathrm{depth}} + \mathcal{L}_{\mathrm{point}} + \lambda \mathcal{L}_{\mathrm{track}} $$ $\lambda$ 论文取 $0.05$. 用 AdamW 优化器优化模型, 直至收敛.

Spatial-MLLM

大多数现有的 MLLM 在其视觉编码器的预训练中主要使用图像-文本对, 遵循了 CLIP的范式. 这使得视觉编码器在捕捉高层语义内容方面表现出色, 但在仅使用 2D 视频输入时缺乏结构和空间信息. 因此, 论文 [] Unknown-material 提出了一个新的 空间 MLLM (Spatial-MLLM) 模型, 旨在通过引入空间感知能力来增强 MLLM 的视觉理解和推理能力.

算法Spatial-MLLM 输入 > 一段视频序列 $\{f_i\}_{i=1}^{N_k}$. 输出 > 给下游 LLM 的 token 序列. 引入 2D 编码器 $\mathcal{E}_{\mathrm{2D}}$, 采用 Qwen2.5-VL 相同设计, 将输入帧编码为语义丰富的特征: $$ \mathbf{e}_{\mathrm{2D}} = \mathcal{E}_{\mathrm{2D}}\left(\{\mathbf{f}_i\}_{i=1}^{N_k}\right) \in \mathbb{R}^{N_k' \times \left\lfloor \frac{H}{p_{\mathrm{2D}}} \right\rfloor \times \left\lfloor \frac{W}{p_{\mathrm{2D}}} \right\rfloor \times d_{\mathrm{2D}}} $$ 其中 $p_{\mathrm{2D}}$ 是 2D 编码器的 patch 大小, $d_{\mathrm{2D}}$ 是输出特征的维度, 连续的两帧被分组作为视频输入, 因此 $N_k'=N_k/2$. 引入空间编码器 $\mathcal{E}_{\mathrm{spatial}}$, 采用 VGGT 的特征骨干网络. $$ \mathbf{e}_{\mathrm{3D}}, \mathbf{e}_c, \mathbf{e}_{\text{register}} = \mathcal{E}_{\text{spatial}}\left(\{\mathbf{f}_i\}_{i=1}^{N_k}\right), \quad \mathbf{e}_{\mathrm{3D}} \in \mathbb{R}^{N_k \times \left\lfloor \frac{H}{p_{\mathrm{3D}}} \right\rfloor \times \left\lfloor \frac{W}{p_{\mathrm{3D}}} \right\rfloor \times d_{\mathrm{3D}}} $$ 其中 $e_{\mathrm{3D}}$ 是空间特征, $e_c$ 是相机特征, $e_{\text{register}}$ 是寄存器 token. 在空间和时间维度上对齐 $e_{\mathrm{2D}}$ 和 $e_{\mathrm{3D}}$: $$ \mathbf{e}_{3\mathrm{D}}' = \text{Rearrange}(\mathbf{e}_{3\mathrm{D}}), \quad \mathbf{e}_{3\mathrm{D}}' \in \mathbb{R}^{N_k' \times \left\lfloor \frac{H}{p_{2\mathrm{D}}} \right\rfloor \times \left\lfloor \frac{W}{p_{2\mathrm{D}}} \right\rfloor \times d_{3\mathrm{D}}'} $$ 使用两个简易的 MLP 把两个信息连接成统一的 token. $$ \mathbf{e} = \text{MLP}_{2\mathrm{D}}(\mathbf{e}_{2\mathrm{D}}) + \text{MLP}_{3\mathrm{D}}(\mathbf{e}_{3\mathrm{D}}') \in \mathbb{R}^{S \times d_{\mathrm{LLM}}} $$ 这里 $S = N_k' \times \left\lfloor \frac{H}{p_{2\mathrm{D}}} \right\rfloor \times \left\lfloor \frac{W}{p_{2\mathrm{D}}} \right\rfloor$ 是 token 长度.

由于显存限制, MLLM 只能处理场景视频序列中的一小部分帧. 关于帧采样广泛的做法是均匀帧采样, 论文设计了一个简单的空间感知帧采样策略.

算法Spatial-MLLM 帧采样 输入 > 一个场景视频 $\mathcal{V} = \{f_i\}_{i=1}^{N}$. 输出 > 选择其中的 $N_k$ 帧 $\{ f_i^k \}_{i=1}^{N_k}$ 使其尽可能多地覆盖场景. 均匀采样 $N_m$ 帧 $\{ f_i^m \}_{i=1}^{N_m}$, 其中 $N_m \in (N_k, N)$. 利用 $\mathcal{E}_{\mathrm{3D}}$ 提取对应 3D 特征 $\mathbf{e}^m_{3\mathrm{D}}$ 和相机特征 $\mathbf{e}^m_c$. 使用 VGGT 模型预训练的相机预测头 $f_c$ 和 $f_d$ 来解码一组相机参数和深度图: $$ \{\mathbf{E}_i^m, \mathbf{K}_i^m\}_{i=1}^{N_m} = f_c(\mathbf{e}_c), \quad \text{and} \quad \{\mathbf{D}_i^m\}_{i=1}^{N_m} = f_d(\mathbf{e}_{3\mathrm{D}}) $$ 由此的得到每个帧在场景中能覆盖的体素 $V(f_i^m)$, 因此转化为从中选取元素最大化覆盖 $\left| \cup_{i=1}^{N_k} V(f_i^k) \right|$ 问题. 特别地论文采用贪心策略加快速度.

显然, 在选取之后可以直接利用得到的 $\mathbf{e}_{\mathrm{3D}}$ 而无需重新计算.

在下游任务中, $\mathcal{E}_{\mathrm{2D}}$ 和 $\mathcal{E}_{\mathrm{3D}}$ 都是预训练好的, 参数冻结, 只训练 MLP 连接层和 LLM. 论文采用先 SFT 再 RL (GRPO) 的方式进行训练.

参考文献

Alexey Dosovitskiy, Lucas Beyer, Alexander Kolesnikov, Dirk Weissenborn, Xiaohua Zhai, Thomas Unterthiner, Mostafa Dehghani, Matthias Minderer, Georg Heigold, Sylvain Gelly, Jakob Uszkoreit, and Neil Houlsby. An image is worth 16x16 words: Transformers for image recognition at scale. ICLR, 2021.
Maxime Oquab, Timothee Darcet, Theo Moutakanni, Huy V. Vo, Marc Szafraniec, Vasil Khalidov, Pierre Fernandez, Daniel HAZIZA, Francisco Massa, Alaaeldin ElNouby, Mido Assran, Nicolas Ballas, Wojciech Galuba, Russell Howes, Po-Yao Huang, Shang-Wen Li, Ishan Misra, Michael Rabbat, Vasu Sharma, Gabriel Synnaeve, Hu Xu, Herve Jegou, Julien Mairal, Patrick Labatut, Armand Joulin, and Piotr Bojanowski. DINOv2: Learning robust visual features without supervision. Transactions on Machine Learning Research, 2024. 2, 4, 11
Timothee Darcet, Maxime Oquab, Julien Mairal, and Piotr Bojanowski. Vision transformers need registers. arXiv preprint arXiv:2309.16588, 2023. 4
Rene Ranftl, Alexey Bochkovskiy, and Vladlen Koltun. Vision transformers for dense prediction. In Proceedings of the IEEE/CVF international conference on computer vision, pages 12179–12188, 2021. 3, 5, 11
Alex Kendall and Roberto Cipolla. Modelling uncertainty in deep learning for camera relocalization. In Proc. ICRA. IEEE, 2016. 5
Nikita Karaev, Ignacio Rocco, Ben Graham, Natalia Neverova, Andrea Vedaldi, and Christian Rupprecht. CoTracker: It is better to track together. In Proceedings of the European Conference on Computer Vision (ECCV), 2024. 3, 5, 6, 9, 10
S. Bai, K. Chen, X. Liu, J. Wang, W. Ge, S. Song, K. Dang, P. Wang, S. Wang, J. Tang, H. Zhong, Y. Zhu, M. Yang, Z. Li, J. Wan, P. Wang, W. Ding, Z. Fu, Y. Xu, J. Ye, X. Zhang, T. Xie, Z. Cheng, H. Zhang, Z. Yang, H. Xu, and J. Lin, “Qwen2.5-vl technical report,” ArXiv, vol. abs/2502.13923, 2025.