测试时强化学习
TTA
通常情况下, 深度学习模型在训练完成后就固定了参数, 在测试或部署阶段不再更新. 但在实际应用中, 测试数据可能与训练数据的分布存在差异, 导致模型性能下降. 因此后续的微调显得非常重要.
定义
测试时适应 (Test-time Adaption, TTA) 算法指在不使用真实标签的前提下, 利用当前测试样本或其增强版本来在线微调模型, 使其更适应当前的输入分布.
常见的测试时适应算法包括:
过往的 TTA 算法一般基于无监督学习, 即便是强化学习算法, 需要辛苦设计奖励函数, RLHF 需要人工标注数据, 成本高昂.
TTRL
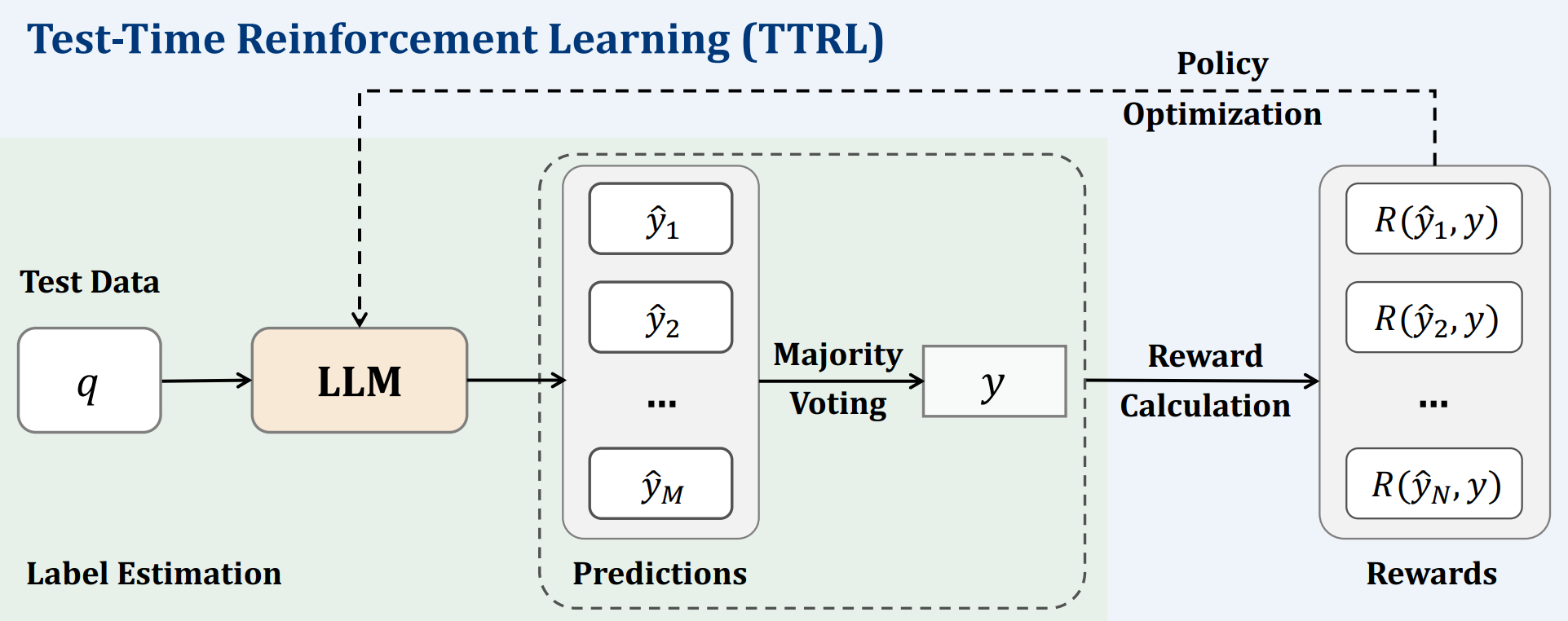
论文 [] Unknown-material 开创性地提出了 测试时强化学习 (Test-Time Reinforcement Learning, TTRL) 算法 (后面几篇论文都是在此基础上进行改进). TTRL 通过强化学习的方式, 在测试时对模型进行微调, 使其更好地适应当前输入分布.
在 无监督 的情况下, 怎么设置奖励函数? 论文的策略非常简单: 多数投票.
算法TTRL
输入 > 一个模型 $f_{\theta}$, 测试样本 $x$.
输出 > 微调后的模型 $f_{\theta'}$.
- 对输入 $x$ 做多次预测, 得到预测结果 $y_i$.
- 统计每个预测结果的出现次数, 设最常见的预测结果为 $y^*$, 称为一致动作.
- 计算奖励函数 $R(y_i)$: $$ R(y_i) = \mathbb{I}(y_i = y^*) $$
- 通过梯度上升更新模型参数 $\theta$ 为 $\theta'$: $$ \theta' = \theta + \eta \nabla_{\theta} \mathbb{E}_{y_i \sim f_{\theta}(x)}[R(y_i)] $$
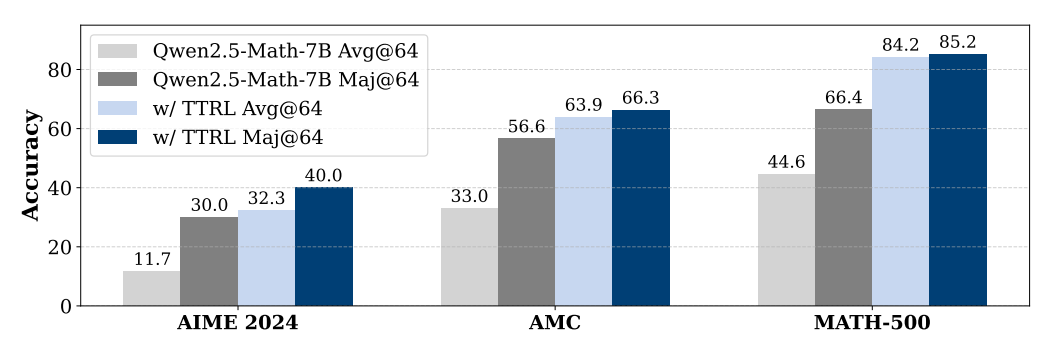
效果非常显著, 甚至可以与带有有一定数据泄漏的监督方案相媲美.
为什么能做这么好? 论文 [] 给出了三个原因:
- 标签估计: TTRL 引入标签估计, 尽管存在不确定性, RL 仍具有一定鲁棒性, 且通常比 SFT 具有更好的泛化能力.
- 奖励函数设计: “幸运命中” (lucky hit) 现象, 即便预测不准确, 只要估计标签与预测答案不同, 验证器就能分配正确的 $0$ 奖励. 实验表明, 尽管多数投票的标签估计可能不准确, 但奖励函数的估计却非常准确. 原因是模型输出概率非常分散, 因此即使标签未被准确估计, 由于 “幸运命中”, 大多数输出仍然可以收到正确的奖励.
- 在线学习: TTRL 是在线学习算法, 可以在测试时不断更新模型参数, 使其更好地适应当前输入分布.
基于熵最小化的强化学习
论文 [] Unknown-material 给出基于最小化熵的强化学习算法 (Reinforcement Learning via Entropy Minimization, RENT). 基于 GRPO 框架测试, 把奖励函数设置为负熵, 认为只通过最小化输出的熵, 即可提高模型推理能力.
$$ R(o) = -\mathcal{H}(p_{\pi_{\theta}}(\cdot|o)) = -\sum_{i=1}^{|V|} p_{\pi_{\theta}}(i|o) \log p_{\pi_{\theta}}(i|o) $$

内部反馈的强化学习
除了 KL 正则化等等项之外, 我们关心奖励函数的设计. 这个奖励要与任务无关, 而由模型内部的反馈来决定. 与 [] 提出的负熵奖励不同, 论文 [] Unknown-material 给出了另一个置信度函数:
$$ R(o) = \frac{1}{|o|}\sum_{i=1}^{|o|}KL(U \| p_{\pi_{\theta}}(\cdot|o_{\lt i})) = -\frac{1}{|o| \cdot |V|} \sum_{i=1}^{|o|}\sum_{j=1}^{|V|} \log \left( |V| \cdot p_{\pi_{\theta}} (j|o_{\lt i}) \right) $$其中 $o$ 是 token 序列, $U$ 表示均匀分布.
带有 CLIP 反馈的强化学习
对于一般任务, 传统的测试时适应算法要最小化熵, 但很显然这个方式容易陷入错误的模型预测中. 与监督微调模型相比, 带有反馈的学习模型有更好的泛化能力.
CLIP
文章 [] Unknown-material 通过引入 CLIP 反馈来解决置信度过高问题, 称为 RLCF(如下图).

除了分类任务外, 通过特定任务的采样策略和适当的选择奖励基线, RLCF 可以很容易地扩展到不仅仅是检索这样的区分任务, 还可以扩展到图像字幕这样的泛化任务.
我们现在关心视觉语言模型 (VLM), 因此要衡量跨模态的相似性. 对比语言-图像预训练 (Contrastive Language-Image Pre-training, CLIP) 模型通过对图像和文本进行编码, 使得它们在同一个共享的向量空间中具有相似的表示.
算法CLIP
输入 > 图像 $v$ 和文本 $t$.
输出 > 图像和文本的相似度分数 $s(v,t)$.
- CLIP 训练两个编码器: 图像编码器 $g$ 和文本编码器 $h$.
- 二者的输出分别为 $g(v)$ 和 $h(t)$.
- 计算相似度分数, 常用的是余弦相似度: $$s(v,t) = \frac{g(v) \cdot h(t)}{\|g(v)\| \|h(t)\|}$$
- 返回相似度分数 $s(v,t)$.
RLCF 算法
对于 VLM, 训练集 $\mathcal{D}_\mathrm{train}$ 和测试集 $\mathcal{D}_\mathrm{test}$ 都是图像和文本对 $(v,t)$ 的集合. 需要注意, 算法的微调是在 单个 测试样本上进行的.
对于奖励函数 $R$, 我们希望学习到最好的概率分布 $f_{\theta}(v) = [p(t|v,\theta)]_{t \in T}$ 使得其能最大化奖励:
$$\max_{\theta} \mathbb{E}_{t \sim f_{\theta}(v)}R(t,v)$$我们正式引入 带有 CLIP 反馈的强化学习 (Reinforcement Learning with CLIP Feedback, RLCF) 算法.
算法RLCF (分类任务)
输入 > 一个已经训练好的 VLM 模型 $f_{\theta}$, 测试样本 $v$.
输出 > 微调后的模型 $f_{\theta'}$.
- 对测试样本 $v$ 进行数据增强, 生成多个增强样本 $\tau_i(v)$.
- 按照 CLIP 的编码器编码 $v$ 和 $\tau_i(v)$, 计算当前模型的预测 $P(t|v,\theta)$. 注意此时训练文本应当是类似于 prompt + label 的形式, 如 “a photo of a cat”.
- 做置信度筛选, 只保留预测熵足够低的样本 $\tau_i(v)$. 在这些样本中, 按照 top-K 策略选择预测结果, 得到 K 对文本和图像 $(\tau_i(v), t_j)_{j=1}^K$. 暂记为 $(v,t)$ 以进行后续计算.
- 按照先前的工作, 根据 CLIP 模型计算 CLIPScore: $$ \mathrm{CLIP-S}(t,v) = w \times \max(\mathrm{CLIP}(t,v), 0) $$ 其中 $w=2.5$ 是一个常数.
- 由于 CLIPScore 永远是非负的, 加入一个奖励基线增加稳定性: $$ R(t,v) = \mathrm{CLIP-S}(t,v) - \mathbb{E}_{t' \sim f_{\theta}(v)}[\mathrm{CLIP-S}(t',v)] $$
- 通过 REINFORCE 策略梯度更新模型参数 $\theta$ 为 $\theta'$, 使得模型能够最大化奖励, 注意此时 只 更新图像编码器 $g$ 的参数: $$ \nabla_{\theta} \mathbb{E}_{t \sim f_{\theta}(v)}[R(t,v)] = \mathbb{E}_{t \sim f_{\theta}(v)}[R(t,v) \nabla_{\theta} \log f_{\theta}(t|v, \theta)] $$
- 返回微调后的模型 $f_{\theta'}$.

相较于监督学习, 基于反馈的强化学习更加通用, 例如可以进行图像描述的任务.
算法RLCF (图文转换)
基本可以从上面的 RLCF 算法中直接泛化修改. 只需要注意如果是文本生成图片时, 应该固定图像编码编码器 $g$ 而微调文本编码器 $h$, 且此时不做数据增强.

技巧和变体
- 使用多个奖励模型及权重: 默认情况下, 使用单个 CLIP-ViT-L/14. 可以使用多个 CLIP 模型, 并对它们的输出进行加权平均, 以获得更好的奖励信号.
- 片段式测试时适应 (Episodic TTA): 假定模型泛化能力很强, 测试时只在测试集上微调, 随后丢弃重置为原参数 $\theta^*$, 防止污染大模型.
- 动量缓冲 (Momentum Buffer): 尽管片段式测试时适应确保可靠性, 但影响了模型增量学习能力. 因此引入一个动量缓冲, 在每次 TTA 中, 按照移动平均的方式更新缓冲 $\xi \leftarrow m\xi + (1-m)\theta$, 每经过若干次样本后, 再将缓冲 $\eta$ 作为新的参数 $\theta$ 进行更新.
实验
RLCF 方法可以通用地建立在常用的架构上. 在零样本分类任务, 零样本图文检索和图像描述任务上, RLCF 都能显著提升模型的性能.
引入协方差正则化的强化学习
与论文 [] 不同, 论文 [] Unknown-material 通过熵动力学来研究熵崩溃的问题, 最终的目的依然是控制熵.
熵崩溃
强化学习过程中对于高置信度的策略会愈发增强其使用概率, 导致熵变得更加降低. 以下图揭示了熵崩溃和性能饱和的关系. 当熵下降到某个阈值时, 性能会达到饱和点.

论文定量分析认为, 如果没有像熵损失或者 KL 散度这样的正则化, 下游性能完全可以通过策略熵来预测, 精确来说可以拟合成指数函数:
$$ R = -a \exp(\mathcal{H}) + b $$$R$ 是验证集的性能, $\mathcal{H}$ 是策略的熵.
熵-性能函数
这个函数可以用来分析模型的性能和熵之间的关系, 有几个特点:
- 系数与算法无关: 下面这个图几个算法得到的曲线是类似的, 这表明 $a,b$ 可能是模型和数据的固有属性.

- 预测不同模型的函数系数: 显然 $a$ 是模型将熵转化为下游性能的速度. $−a+b$ 是当熵归零时模型可以达到的最大验证性能. 理论上个更大的性能应该对应更大的 $a$ 和 $b$. 此外不同的任务也会有不同的系数
系数 $a$ 系数 $b$ 数学任务 

代码任务 

总结, 在策略熵减少过程中, 性能天花板不仅存在, 而且可以被预测.
熵动力学
我们主要关注相邻两次迭代的熵变化 $\mathcal{H}(\pi_{\theta}^{k+1}) - \mathcal{H}(\pi_{\theta}^{k})$.
定理策略梯度下的熵变化
令行为策略 $\pi_{\theta}$ 为一个 softmax 策略, 并通过标准策略梯度更新, 两个连续步骤中给定状态 $s$ 的策略熵之差满足:
$$ \mathcal{H}(\pi_{\theta}^{k+1}|s) - \mathcal{H}(\pi_{\theta}^{k}|s) \approx -\eta \mathrm{Cov}_{a \sim \pi_{\theta}^{k}(\cdot|s)} \left( \log \pi_{\theta}^{k}(a|s), \pi_{\theta}^k(a|s) \cdot A(s,a) \right) $$定理自然策略梯度下的熵变化
令行为策略 $\pi_{\theta}$ 为一个 softmax 策略, 并通过标准策略梯度更新, 两个连续步骤中给定状态 $s$ 的策略熵之差满足:
$$ \mathcal{H}(\pi_{\theta}^{k+1}|s) - \mathcal{H}(\pi_{\theta}^{k}|s) \approx -\eta \mathrm{Cov}_{a \sim \pi_{\theta}^{k}(\cdot|s)} \left( \log \pi_{\theta}^{k}(a|s), A(s,a) \right) $$揭示了当前策略下的动作概率 $P(a)$ 与相应的优势函数 $A(a)$ 之间的强正相关性. 作者做了实验验证了这个定理估计的正确性.
协方差正则化
论文认为直接采用传统强化学习中的熵正则化技术难以解决 LLMs 的熵瓶颈问题, 过高的熵正则化甚至会导致熵爆炸.
实验表明, 小部分 token 的协方差极高, 在触发熵崩溃中占据了主导地位. 受到 PPO 策略的启发, 论文提出两种协方差感知方法: Clip-Cov 和 KL-Cov.
对于 token $y_i$ 的协方差, 定义为:
$$ \mathrm{Cov}(y_i) = \left( \log \pi_{\theta}(y_i) - \mathbb{E}_{i \in [N]}\left[ \log \pi_{\theta}(y_i) \right] \right) \left(A(y_i) - \mathbb{E}_{i \in [N]}\left[A(y_i)\right]\right) $$算法Clip-Cov
输入 > 策略 $\pi_{\theta}$, 协方差阈值 $\omega_l, \omega_h$ (两个都远超均值), 剔除比例 $r$.
输出 > 更新后的策略 $\pi_{\theta'}$.
- 计算每个 token 的协方差 $\mathrm{Cov}(y_i)$.
- 从 $y_i$ 中随机选取 $r \cdot N$ 个满足 $\omega_l \le \mathrm{Cov}(y_i) \le \omega_h $ 的 token, 设索引集为 $I_{\mathrm{clip}}$.
- 将选择的这些 token 从策略梯度中移除, 其余仍然正常更新: $$ L_{\mathrm{clip}}(\theta) = \begin{cases} \mathbb{E}\left[ \frac{\pi_{\theta'}(y_i)}{\pi_{\theta}(y_i)} A(y_i) \right] & \text{if } i \notin I_{\mathrm{clip}} \\ 0 & \text{if } i \in I_{\mathrm{clip}} \end{cases} $$
算法KL-Cov
输入 > 策略 $\pi_{\theta}$, 剔除比例 $k\ll 1$.
输出 > 更新后的策略 $\pi_{\theta'}$.
- 计算每个 token 的协方差 $\mathrm{Cov}(y_i)$.
- 从 $y_i$ 选取方差最大的 $k \cdot N$ 个 token, 设索引集为 $I_{\mathrm{KL}}$.
- 将选择的这些 token 在策略梯度中施加 KL 惩罚: $$ L_{\mathrm{KL}}(\theta) = \begin{cases} \mathbb{E}\left[ \frac{\pi_{\theta'}(y_i)}{\pi_{\theta}(y_i)} A(y_i) \right] & \text{if } i \notin I_{\mathrm{KL}} \\ \mathbb{E}\left[ \frac{\pi_{\theta'}(y_i)}{\pi_{\theta}(y_i)} A(y_i) \right] - \beta KL(\pi_{\theta}(y_i) || \pi_{\theta'}(y_i)) & \text{if } i \in I_{\mathrm{KL}} \end{cases} $$
实验
与一般的熵正则化方法相比, 协方差正则化方法在多个任务上都能显著提升模型性能. 且能一定程度上避免瓶颈问题.
| 策略熵 | LLM 响应长度 | 准确率 | |
|---|---|---|---|
| Qwen-7B |
 |
 |
 |
| Qwen-32B |
 |
 |
 |
测试时样本特定语言模型优化
论文 [] Unknown-material 提出了 测试时样本特定语言模型优化 (Sample-specific Language Model Optimization at Test-time, SLOT) 算法.
算法SLOT
输入 > 预训练语言模型 $f_{\theta}$, 输入 token 序列 $x=(x_1, x_2, \ldots, x_n)$, 优化步数 $T$.
输出 > 拓展生成的文本 $x$.
- 初始化样本特定参数 $\delta=\mathbf{0}\in \mathbb{R}^{1 \times d}$.
- 计算最后一层的隐藏特征 $H = f_{\mathrm{pre}}(x) \in \mathbb{R}^{n \times d}$.
- 修改 $H' = H + \delta$, 这里是广播加法.
- 计算 logits $L = W_{\mathrm{LM}} H' \in \mathbb{R}^{n \times |V|}$ 和其对应的交叉熵损失 $\mathcal{L}$, 并根据损失 $\mathcal{L}$ 优化 $\delta$.
- 重复步骤 2-4, 直到达到优化步数 $T$, 最后得到 $\delta_{\mathrm{opt}}$.
- 计算最后一个 token 的隐藏特征 $H_{\mathrm{last}} = f_{\mathrm{pre}}(x) [-1] \in \mathbb{R}^{1 \times d}$.
- 修改 $H_{\mathrm{last}}' = H_{\mathrm{last}} + \delta_{\mathrm{opt}}$.
- 计算下一个 token 的 logits $L_{\mathrm{next}} = W_{\mathrm{LM}} H_{\mathrm{last}}'$, 随后按 softmax 选择下一个 token $x_{\mathrm{next}}$.
- 把 $x_{\mathrm{next}}$ 添加到输入序列 $x$ 中, 并重复步骤 6-8, 直到生成满足条件的文本.

特意把参数 $\delta$ 放在预测头之前, 是为了减小计算量. 称这个增量为 概率向量调制向量 (Logit Modulation Vector, LMV):
$$ \mathrm{LMV} = W_{\mathrm{LM}}\delta \in \mathbb{R}^{|V|} $$测试表明, 与推理过程相关的词如 “think” 和 “reasoning” 在 LMV 的作用下得到了显著增强.

我的理解是和直接插入一层网络的区别是, 这个反向传播只更新 $\delta$ 而不更新模型参数, 且是一次性的, 只在测试时进行微调. 这只是一个测试时微调, 似乎不是强化学习.
虚假奖励也能训练?!
说了这么多, 其实都是在说如何设计奖励函数. 但是, 论文 [] Unknown-material 提出了一个非常反直觉的问题: 即使在使用与正确答案几乎没有或甚至负相关关系的虚假奖励下训练, RLVR 仍能在某些模型中激发强烈的数学推理能力!
论文给出了五种奖励函数:
- 真实标签 (Ground Truth) 奖励: 直接用真实标签作为奖励函数, 这标定了 RLVR 的上限.
- 多数投票 (Majority Vote) 奖励: 通过多数投票的方式估计标签 (标签很可能是错误的), 以此作为奖励函数.
- 格式化 (Format) 奖励: 当模型输出最后包含
\box{}时, 给予奖励, 否则不奖励. 这个奖励函数与正确答案无关. - 随机 (Random) 奖励: 随机生成奖励.
- 错误 (Incorrect) 奖励: 只对错误的答案给予奖励, 正确答案不奖励.
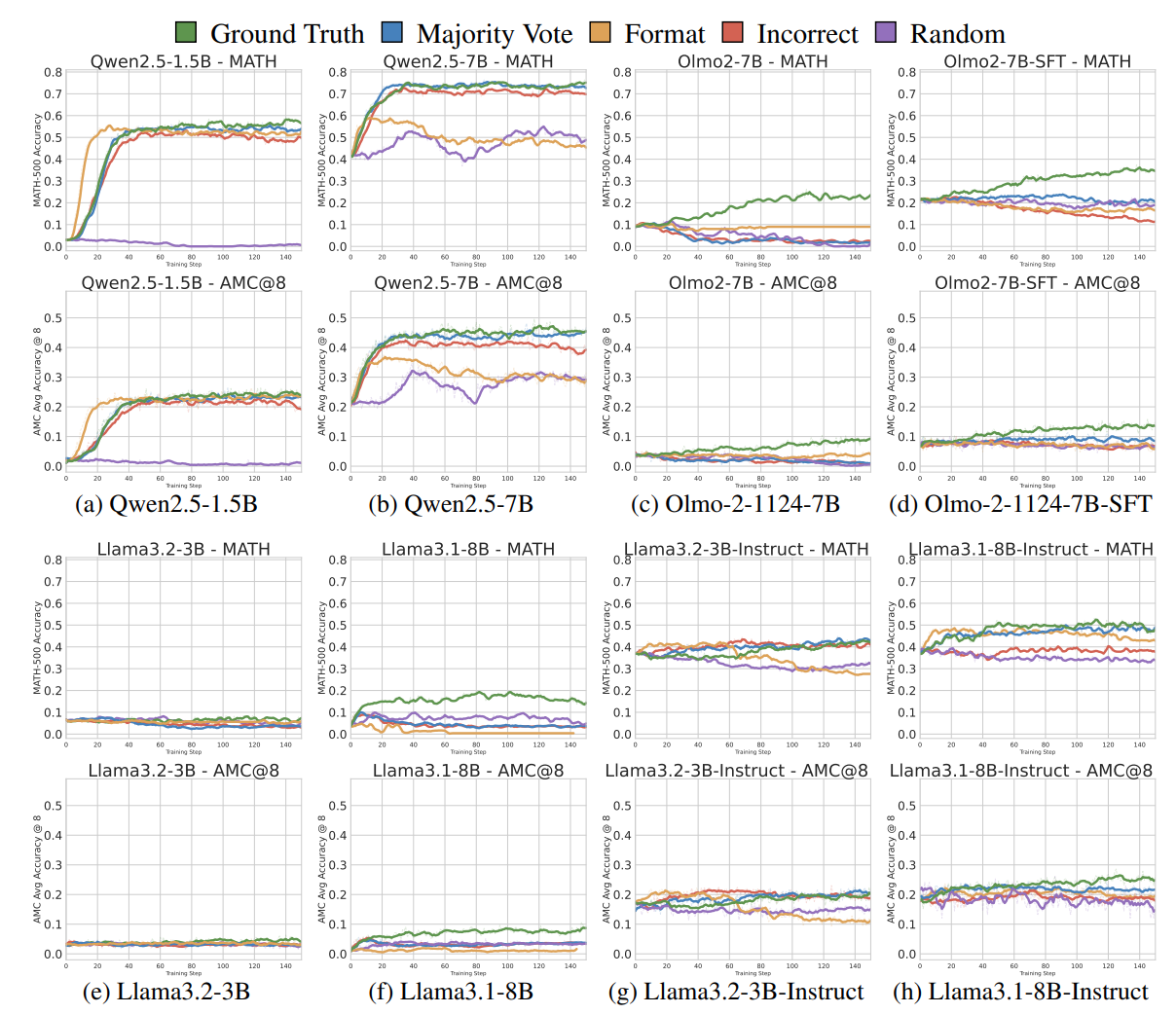
论文围绕了一个小问题展开: 问大模型 $(2,-6)$ 和 $(-4,3)$ 的距离是多少?
不同模型在推理策略上存在先存差异
有些强模型会尝试写 Python 代码来计算距离, 尽管实际上它们并没有代码运行环境. 这种行为称为代码推理 (Code Reasoning), 且实验表明代码推理与准确率呈现强正相关性. 有些弱模型不生成代码, 或者对于代码生成性能弱.
RLVR 在引入虚假奖励时可以增强预存的推理策略
在进行 RLVR 训练后, 代码推理的频率迅速增加, 与准确度提升高度相关; 随机奖励则相对缓慢, 但最终也达到了相似的水平. 此后随着模型自然语言推理准确度的提高, 这一频率逐渐下降, 这表明模型正在从高质量的真实标签奖励中学习真正的知识.
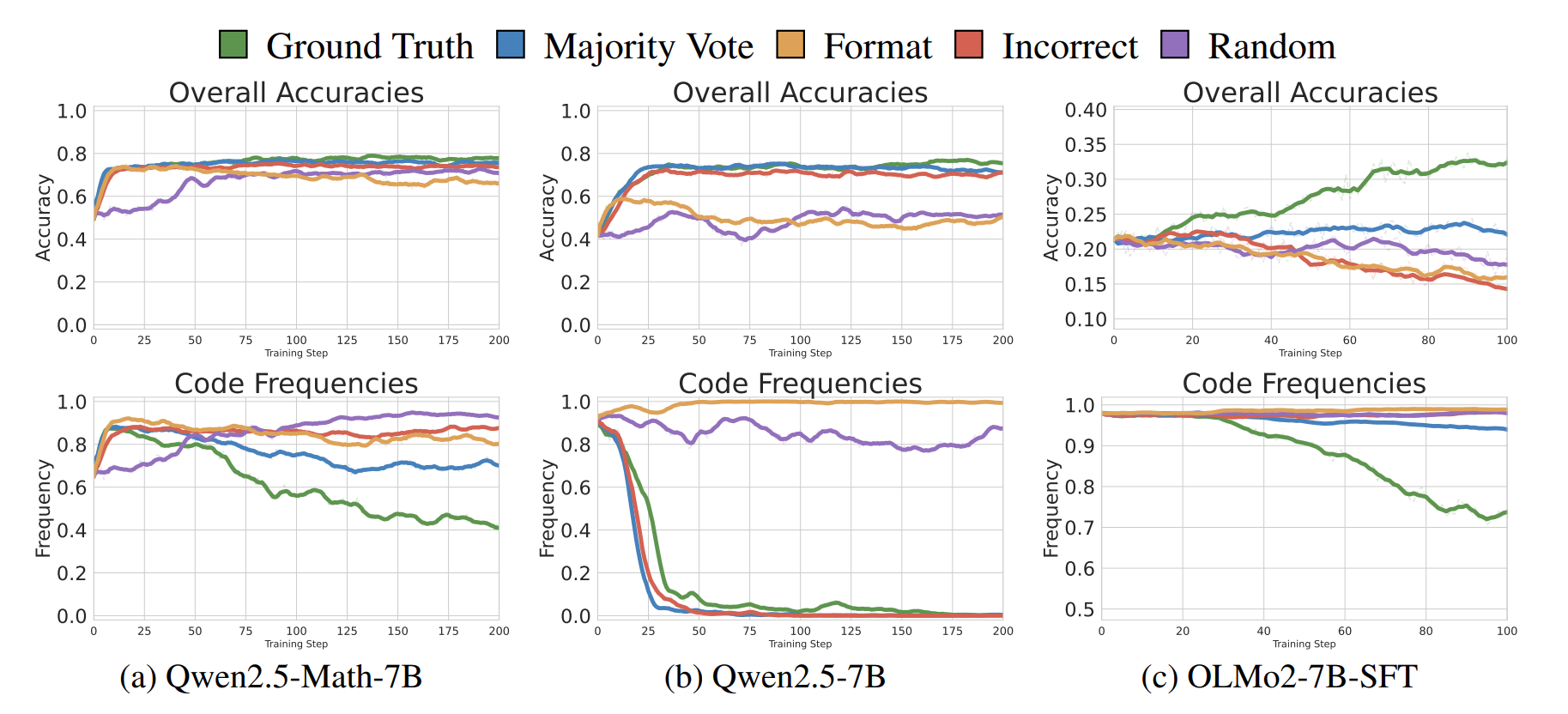
推理策略切换对性能的细化影响
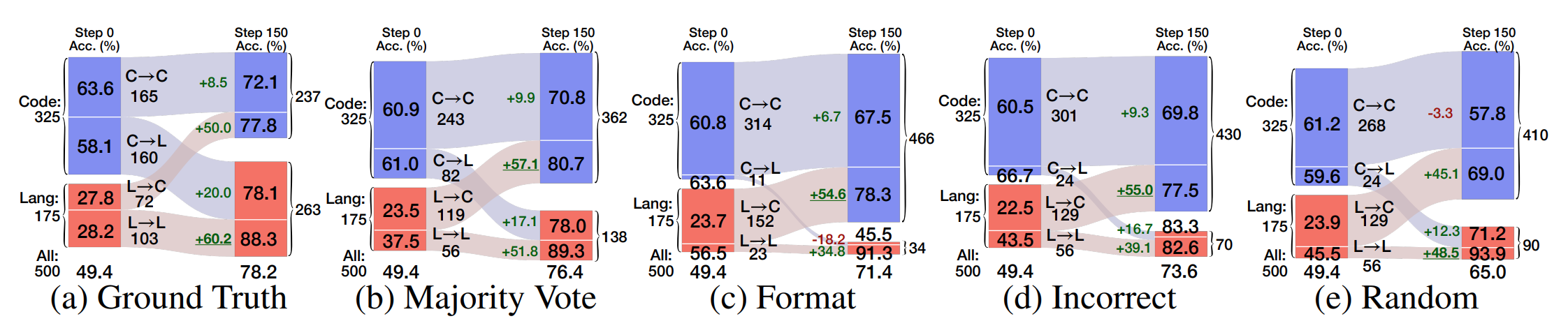
对于所有较弱和虚假的奖励, 模型在 RLVR 后更倾向于使用代码推理. 虚假奖励上的准确度提升主要是通过激发模型使用正确的推理策略实现的.
随机奖励与策略裁剪
关于随机奖励的问题, 论文证明了尽管优势期望值为零, 但由于损失函数中的 clip 机制, GRPO 损失的期望梯度并非为零.
为了验证这个想法, 论文进行了一组对比, 同样使用随机奖励, 区别是是否进行 $(1-\epsilon, 1+\epsilon)$ 重要性采样比裁剪. 结果表明, 在没有裁剪的情况下, 随机奖励不能给模型带来任何提升.
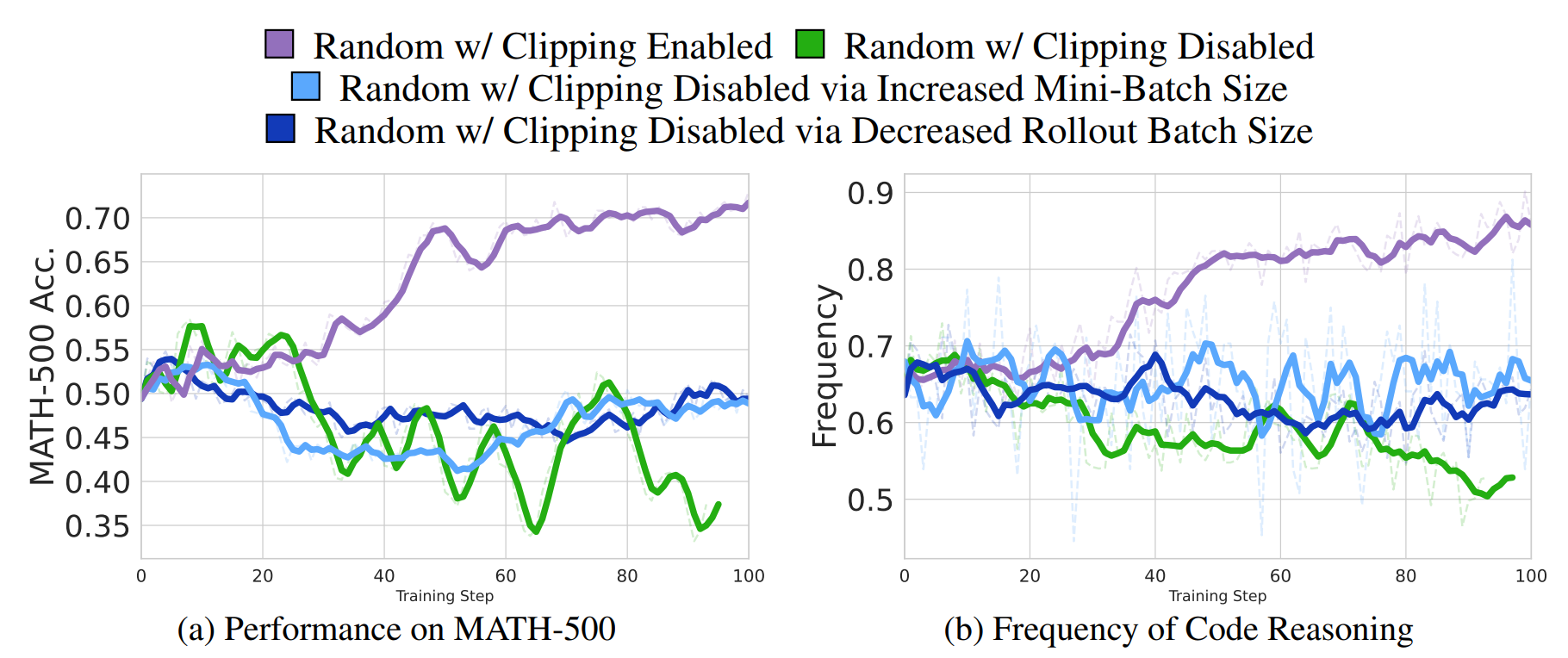
因此综合来看, 论文推测, 在随机奖励训练中, 看似 “训练信号” 实际上是优化算法偏向利用预训练中学习到的先验知识的结果.
Sherlock: 自我纠正推理
论文 [] Unknown-material 指出, 使用 SFT 或 RL 训练的模型缺乏逐步和响应层面自我纠正的能力. 一旦出现错误, 模型难以修正其推理, 往往无法从错误中恢复.
自我纠正
对于推理模型, 自我纠正行为可以有两种实现方式:
-
逐步骤纠正: 模型在其单次思考过程中反思其之前的第 i 步错误, 并对其进行修正:
$$ (r, y_{i+1}, \cdots, y_n; a) \sim \pi(\cdot| x_{I \& T}; y_1, \cdots, y_i^*) $$其中 $y_i$ 代表第 $i$ 步推理, $a$ 是最终答案, $r$ 是模型的反思提示词 (如 “但是”, “等等”), $x_{I \& T}$ 是输入的图像和文本, $y_i^*$ 是错误的推理.
-
逐响应纠正: 模型尝试纠正其之前的错误响应:
$$ (y_1^2, \cdots, y_n^2; a) \sim \pi(\cdot| x_{I \& T}; y_1^1, \cdots, y_n^1; t) $$其中 $y^j, a^j$ 是模型的第 $j$ 次尝试响应.
Sherlock
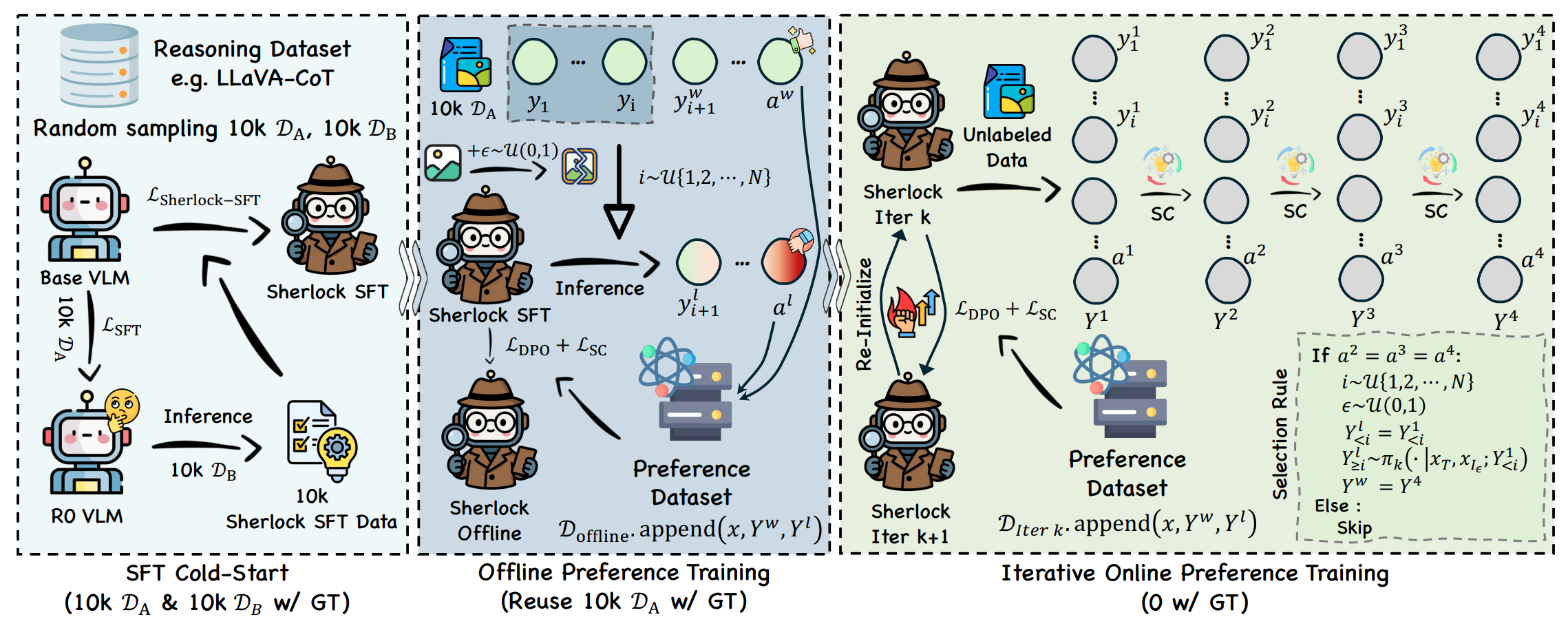
为解决这一局限, 论文 [] 引入所谓 Sherlock 算法来教导模型自我纠正, 从而增强其推理能力.
算法Sherlock
I: SFT 冷启动
- 从已知数据集中随机采样样本, 形成训练集 $\mathcal{D}_A$; 再次采样形成 $\mathcal{D}_B$, 这些样本包含高质量的 COT.
- 在 $\mathcal{D}_A$ 上使用普通监督微调 (SFT) 训练基础 VLM,得到模型 $R0_{\mathrm{VLM}}$。
- 对于每个样本 $(x_{I\&T}, Y^w)$ 在 $\mathcal{D}_B$ 中, 保留原本标签 $Y^w$, 同时用 $R0_{\mathrm{VLM}}$ 生成一个推理轨迹 $Y^l$, 组合成新数据集 $\mathcal{D}_{\mathrm{Sherlock}} = (x_{I\&T}, Y^w, Y^l)$。
- 使用如下公式中的损失函数, 联合 直接生成 (Direct Generation) 和 自我纠正 (Self-Correction) 两个任务.:
II. 离线偏好训练
现在对于初始轨迹 $Y^1 = (y_1^1, \cdots, y_n^1;a^1)$, 我们假定此时已经有一部分推理正确, 需要在生成一个更好的轨迹 $Y^2 = (y_1^2, \cdots, y_n^2;a^2)$.
-
随机在 $1 \sim n$ 中采样一个整数 $i$, 此时我们假定 $Y^1_{\lt i}$ 是正确的, 希望生成更好的 $Y^2_{\ge i}$.
-
按照如下公式:
$$ \max_{\pi}\mathbb{E}_{Y_{\geq i}^{2}\sim\pi(\cdot|[x_{I\&T},Y^{1},t;Y_{\lt i}^{2}])}\left[p(Y_{\geq i}^{2}\succ Y_{\geq i}^{1}|x_{I\&T};Y_{\lt i}^{2})-\beta D_{\mathrm{KL}}(\pi\|\pi_{\mathrm{ref}}|[x_{I\&T},Y^{1},t;Y_{\lt i}^{2}])\right]\\+\mathbb{E}_{Y_{\geq i}^{2}\sim\pi(\cdot|[x_{I\&T},Y^{1},t;Y_{\lt i}^{1}])}\left[p(Y_{\geq i}^{2}\succ Y_{\geq i}^{1}|x_{I\&T};Y_{\lt i}^{1})-\beta D_{\mathrm{KL}}(\pi\|\pi_{\mathrm{ref}}|[x_{I\&T},Y^{1},t;Y_{\lt i}^{1}])\right] $$$t$ 是一个指令. 即希望 $Y_{\geq i}^{2}$ 在 $Y_{\lt i}^{2}$ 的条件下, 能够比 $Y_{\geq i}^{1}$ 更好, 且与参考模型 $\pi_{\mathrm{ref}}$ 尽量接近. 要最大化此式, 设:
$$ v(x, Y^1, t; Y_{\lt i}^{1}, Y_{\lt i}^{2}; \pi_{\theta}) = \beta \log \rho(Y_{\geq i}^{2} | [x, Y^1, t; Y_{\lt i}^{2}]) - \beta \log \rho(Y_{\geq i}^{1} | [x, Y^1, t; Y_{\lt i}^{1}]) \\ u(x, Y^1, t; Y_{\lt i}^{1}, Y_{\lt i}^{2}; \pi_{\theta}) = \beta \log \rho(Y_{\geq i}^{2} | [x, Y^1, t; Y_{\lt i}^{1}]) - \beta \log \rho(Y_{\geq i}^{1} | [x, Y^1, t; Y_{\lt i}^{2}]) $$其中 $\rho$ 表示 $\pi_{\theta}$ 和 $\pi_{\mathrm{ref}}$ 的重要性采样比, 前一项是鼓励生成更好的轨迹, 后一项是惩罚生成更差的轨迹. 论文证明采用 MSE 误差函数:
$$ \begin{aligned} L_{\mathrm{SC}}(\pi_{\theta}; \pi_{\mathrm{ref}}) &= \mathbb{E}_{(x, Y^w, Y^l) \sim \mathcal{D}} \left[ 1 - v(x_{I\&T}, Y^l, t; Y_{\lt i}^{l}, Y_{\lt i}^{w}; \pi_{\theta}) - u(x_{I\&T}, Y^l, t; Y_{\lt i}^{l}, Y_{\lt i}^{w}; \pi_{\theta}) \right]^2 \\ & + \mathbb{E}_{(x, Y^w, Y^l) \sim \mathcal{D}} \left[ 1 + v(x_{I\&T}, Y^w, t; Y_{\lt i}^{w}, Y_{\lt i}^{l}; \pi_{\theta}) + u(x_{I\&T}, Y^w, t; Y_{\lt i}^{w}, Y_{\lt i}^{l}; \pi_{\theta}) \right]^2 \end{aligned} $$ -
随后再加上 DPO 的损失函数 (前面做的工作已经是偏好优化策略, 再加上这个的目的存疑):
$$ L_{\mathrm{Sherlock}}(\pi_{\theta}; \pi_{\mathrm{ref}}) = L_{\mathrm{SC}}(\pi_{\theta}; \pi_{\mathrm{ref}}) + \alpha L_{\mathrm{DPO}}(\pi_{\theta}; \pi_{\mathrm{ref}}) $$ -
在此过程中可以根究不同的 $i$ 采用不同的 $\beta$:
$$ \beta(i, n, \epsilon) = \frac{1}{4\left( 0.5 + \left( \frac{i}{n} \right)^{0.5 + \epsilon / 2} \right)} $$当截断较早, $i$ 较小, $\beta$ 较大, 使得模型更倾向于靠拢 $\pi_{\mathrm{ref}}$, 产生更谨慎的更新, 反之亦然.
III. 迭代在线偏好训练
在线迭代训练与离线阶段唯一的区别是没有 ground-truth 的回答 $Y^w$.
- 对于每个直接生成的 $Y^1$, 我们进行三轮自我纠正以获得 $Y^2, Y^3, Y^4$.
- 应用自我一致性过滤策略: 如果三个纠正响应的最终答案在语义上相同 ($a^2 = a^3 = a^4$), 则认为 $Y^4$ 是偏好回应, $Y_1$ 是非偏好回应. 否则跳过此次训练.
- 为进一步减小模型偏好优化的噪声, 让初始的 $Y^1$ 变得更差: 维持 $Y^{l}_{\lt i} = Y^{1}_{\lt i}$, 但对于 $Y^{l}_{\ge i}$ 则在 $Y^{1}_{\ge i}$ 的基础上进行扰动.
- 随后按照离线偏好训练的方式继续进行.
实验
论文指出现有的模型并不能通过自我纠正提高推理能力, 经过 Sherlock 进行训练后, 再进行自我纠正, 模型的推理能力有了显著提升.
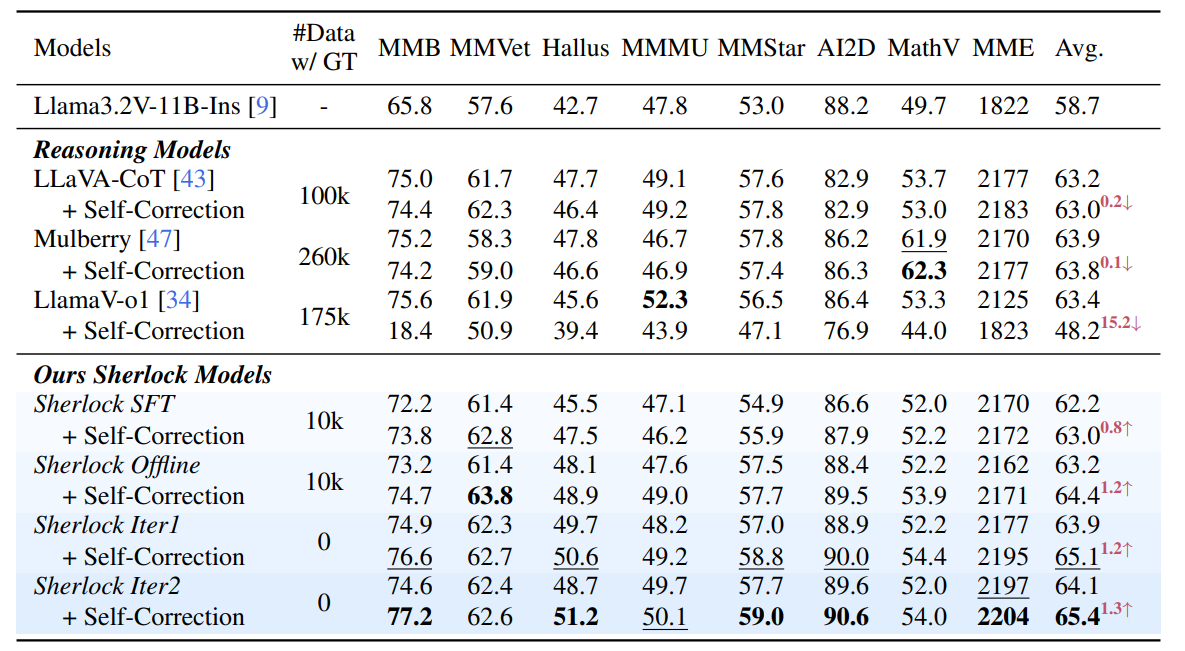
论文进行了消融实验, 验证了 DPO 损失, SC 损失和动态 $\beta$ 的有效性.
Objection!
刚才提及的多数论文都是错的! 一篇未正式发布的文章 [] Unknown-material 要打假, 尤其是有关随机奖励的内容, 批驳的论文如下图:

文章声称, 这是因为预-RL 模型的 Baseline 相比 Qwen 发布的官方数据或其它标准化评估被严重低估了, 在很多情况下,经过 RL 后的模型性能实际上比它们开始时的 (正确评估的) 预-RL Baseline 还要差!
主要问题在于这些论文没有开放数据权重, 导致不能测试, 因而论文的证据不具有说服力. 作者提出了几个可能错误低估的原因:
- 格式: 数学基准测试使用精确匹配评估, 模型需要以特定格式作答, 例如在
\boxed{}内, 有时模型未能遵循格式. 如果模型解决了问题并得到正确答案, 但未能正确格式化, 并不意味着模型的推理能力存在问题. 应该事先通过示例提示或在进行格式演示的少量样本 SFT 来解决 LLMs 的格式问题. - 温度: Qwen3 模型页面 上关于最佳设置有明确的建议. 有几篇论文把温度设置太低, 导致降低准确率.
- 测试规模: 有的论文使用的 Benchmark 规模太小, 方差太大.
- token 长度: 有些模型需要较长的推理流程, 截断较小时会导致模型无法完成响应, 进而降低准确率.
参考文献
- Dequan Wang, Evan Shelhamer, Shaoteng Liu, Bruno Olshausen, and Trevor Darrell. Tent: Fully test-time adaptation by entropy minimization.arXiv preprint arXiv:2006.10726, 2020.